3.1 Geometry

Q1

Topic	3.1 Geometry
Tag
Source	N15-TZ0-P1-1(HL)
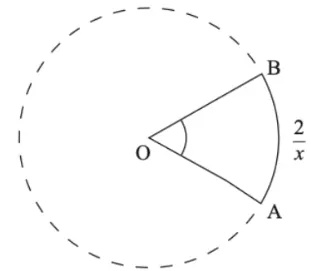
Question Text	The following diagram shows a sector of a circle where $A \hat{O}B=x$ radians and the length of the $\operatorname{arc} A B=\frac{2}{x} \mathrm{~cm}$ . Given that the area of the sector is $54 \mathrm{~cm}^2$ , find the length of the $\operatorname{arc} A B$ .

Total Mark	4
Correct Answer	6
Explanation	na
Mark Scheme	Step 1: Consider the given information Circle sector, arc length $=\frac{2}{x}$ , arc angle $=x$ radians, sector area $=54$ Step 2: Combine the given information Sector area $=\frac{x}{2 \pi} \times \pi r^2=54$ Arc length $=\frac{2}{x}=r x$ So, $r=\frac{2}{x^2}$ Applying this to the sector area $\frac{x}{2 \pi} \times \pi r^2=\frac{2}{x^3}=54$ Giving, $x=\frac{1}{3}$ , arc length $=6 \mathrm{~cm}$ Answer: 6 cm

Q2

Topic	3.1 Geometry
Tag
Source	M15-TZ1-P1-1(HL)
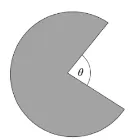
Question Text	The logo, for a company that makes chocolate, is a sector of a circle of radius 5 cm , shown as shaded in the diagram. The area of the logo is $9 \pi \mathrm{~cm}^2$ .

	Diagram not to scale (a) The value of the angle $\theta$ in radians can be expressed as $\frac{a}{b} \pi$ where a and b are positive integers in lowest terms. Find the value of $a+b$ .
Total Mark	3
Correct Answer	57
Explanation	na
Mark Scheme	Area of shaded area $9 \pi=5^2 \pi-5^2 \pi \times \frac{\theta}{2 \pi}$ $\begin{aligned} & \frac{25 \theta}{2}=16 \pi \\ & \theta=\frac{32}{25} \pi \end{aligned}$ Answer: 57
Question Text	(b) Find the total length of the perimeter of the logo. (A) $3 \pi+5$ (B) $3 \pi+10$ (C) $\frac{18 \pi}{5}+5$ (D) $\frac{18 \pi}{5}+10$
Total Mark	2
Correct Answer	D
Explanation	na
Mark Scheme	$\begin{aligned} & \text { arc length }=\frac{18}{25} \pi \times 5 \\ & \text { perimeter }=\frac{18 \pi}{5}+5 \times 2 \\ & \quad=\frac{18 \pi}{5} \pi+10 \end{aligned}$ Answer: D

Q3

Topic	3.1 Geometry
Tag
Source	M19/5/MATHL/HP1/ENG/TZ1/XX/3
Question Text	A sector of a circle with radius $r c m$ , where $r>0$ , has an angle of 2 radian at the centre. Let the area of the sector be $A \mathrm{~cm}^2$ and the perimeter be $P$ cm . Given that $A=P$ , find the value of $r$ .
Total Mark	4
Correct Answer	4
Explanation	na
Mark Scheme	$\begin{array}{lc} & A=P \\ \text { Area of sector }=r^2 \pi \times \frac{\theta}{2 \pi} & \\ \text { Perimeter }=r \theta+2 r & \\ & \frac{1}{2} r^2(2)=r(2)+2 r \\ r^2-4 r=0 \\ & r=4, \text { as } r>0 \end{array}$ Answer: 4

Q4

Topic	3.1 Geometry
Tag
Source	M19/5/MATHL/HP1/ENG/TZ2/XX/8
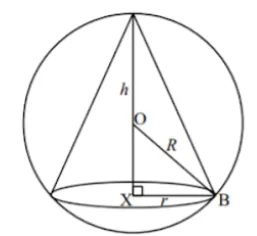
Question Text	A right circular cone of radius $r$ is inscribed in a sphere with centre $O$ and radius $R$ as shown in the following diagram. The perpendicular height of the cone is $h, X$ denotes the centre of its base and B a point where the cone touches the sphere. Given that $R=5, h=9$ , and the value of $V$ can be written as $a \pi$ where a is a positive integer, find the value of $a$ .

Total Mark	4
Correct Answer	27
Explanation	na
Mark Scheme	attempt to use Pythagoras in triangle $OXB$ $r^2=R^2-(h-R)^2=5^2-4^2=3^2$ substitution of $r^2$ into formula for volume of cone $V=\frac{\pi r^2 h}{3}$ $=\frac{\pi \times 9 \times 9}{3}=27 \pi$ Answer: 27