5.5 Application of Integration

Topic	5.5 Applications of integration
Tag	Integration Area Inverse Function Area Between Two Functions Solids of Revolution Kinematics Trigonometric Functions Logarithmic Functions Intercepts By Parts Substitution Partial Fractions Related Rates
Source	N17/5/MATHL/HP1/ENG/TZ0/XX/5
Question Text	A particle moves in a straight line such that at time $t$ seconds $(t \geq 0)$ , its velocity $v$ , in $m s^{-1}$ , is given by $v=8 t e^{-2 t}$ . The exact distance travelled by the particle in the first second can be written as $a-\frac{b}{e^2}$ where $a, b \in \mathbb{Z}^{+}$ . Find the value of $a+b$ .
Total Mark	5
Correct Answer	8
Explanation	na
Mark Scheme	Tip 1: Distance travelled can be found by integrating the velocity at a given time interval. $s=\int_0^1 8 t e^{-2 t} d t$ Tip 2: Notice that integration by parts can be applied $\begin{aligned} & =\left[-4 t e^{-2 t}\right]_0^1-\int_0^1\left(-4 e^{-2 t}\right) d t \\ = & {\left[-4 t e^{-2 t}-2 e^{-2 t}\right]_0^1 } \\ s & =-6 e^{-2}+2=2-\frac{6}{e^2} \end{aligned}$ Answer: $a=2, b=6$

Topic	5.5 Applications of integration
Tag
Source	M16-TZ1-P1-13(HL)
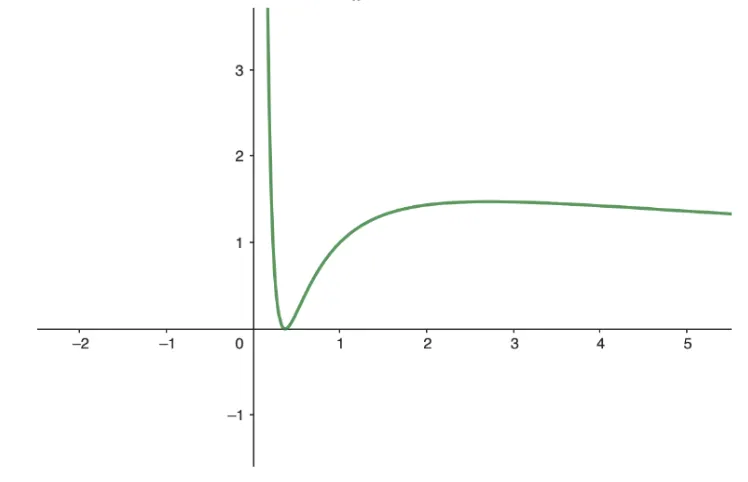
Question Text	The following diagram shows the graph of $y=\frac{(\ln x+1)^2}{x}, x>0$ .

Question Text	The region $R$ is enclosed by the curve, the $x$ -axis and the line $x=e^2$ . (a) Use an appropriate substitution to find the area of region $R$ .
Total Mark	6
Correct Answer	9
Explanation	na
Mark Scheme	Set $\ln x+1=u$ , $\begin{gathered} \frac{d u}{d x}=\frac{1}{x} \\ \int \frac{(\ln x+1)^2}{x} d x=\int u^2 \frac{d u}{d x} d x=\int u^2 d u \end{gathered}$ As $\ln e^2+1=3, \ln (-e)+1=0$ $\text { area }=\left[\frac{1}{3} u^3\right]_0^3=9$ Answer: 9
Question Text	Let $I_n=\int_1^e \frac{(\ln x+1)^n}{x^2} d x, n \in N$ (b) (i) Find the value of $I_0$ . [multuiple choice] (a) 1 (b) $e$ (c) $-\frac{1}{e}$ (d) $1-\frac{1}{e}$ Total Mark : 1 Correct Answer : d Explanation : na Mark Scheme : $I_0=\int_1^e \frac{1}{x^2} d x=\left[-\frac{1}{x}\right]_1^e=1-\frac{1}{e}$ Answer: D (ii) Which statement correctly relates $I_n$ with $I_{n-1}$ ? [multiple choice] (a) $I_n=-\frac{1}{e}+n I_{n-1}$ (b) $I_n=-\frac{2}{e}+1+n I_{n-1}$ (c) $I_n=\frac{1}{e}+n I_{n-1}$ (d) $I_n=\frac{1}{e}+1+n I_{n-1}$ Total Mark : 2 Correct Answer : b Explanation : na Mark Scheme : use of integration by parts $\begin{aligned} & u=(\ln x+1)^n, \frac{d u}{d x}=\frac{n(\ln x+1)^{n-1}}{x}, \frac{d v}{d x}=\frac{1}{x^2}, v=-\frac{1}{x} \\ & I_n=\left[-\frac{1}{x}(\ln x+1)^n\right]1^e+\int_1^e \frac{n(\ln x+1)^{n-1}}{x^2} d x \\ & \\ & I_n=-\frac{2}{e}+1+n I{n-1} \end{aligned}$ Answer: B (iii) Hence find the value of $I_1$ . (a) $2+\frac{1}{e}$ (b) $2+\frac{3}{e}$ (c) $2-\frac{1}{e}$ (d) $2-\frac{3}{e}$ Total Mark : 7 Correct Answer : d Explanation : na Mark Scheme : $\begin{gathered} I_1=-\frac{2}{e}+1+I_0 \\ I_1=-\frac{2}{e}+1+1-\frac{1}{e}=2-\frac{3}{e} \end{gathered}$ Answer: $D$

Topic	5.5 Applications of integration
Tag	Integration Area Inverse Function Area Between Two Functions Solids of Revolution Kinematics Trigonometric Functions Logarithmic Functions Intercepts By Parts Substitution Partial Fractions Related Rates
Source	N16-TZ0-P1-11(HL)
Question Text	Let $y=e^x \cos x$ (a) Find an expression for $\frac{d y}{d x}$ . [multiple choice] (a) $\frac{d y}{d x}=-e^x \sin x$ (b) $\frac{d y}{d x}=e^x \sin x$ (c) $\frac{d y}{d x}=e^x \cos x-e^x \sin x$ (d) $\frac{d y}{d x}=e^x \cos x+e^x \sin x$
Total Mark	2
Correct Answer	c
Explanation	na
Mark Scheme	Using the product rule $\frac{d y}{d x}=e^x \cos x-e^x \sin x$ Answer: C
Question Text	(b) Find an expression for $\frac{d^2 y}{d x^2}$ . (a) $\frac{d^2 y}{d x^2}=2 e^x \sin x$ (b) $\frac{d^2 y}{d x^2}=-2 e^x \sin x$ (c) $\frac{d^2 y}{d x^2}=e^x \cos x-e^x \sin x$ (d) $\frac{d^2 y}{d x^2}=e^x \cos x+e^x \sin x$
Total Mark	2
Correct Answer	b
Explanation	na
Mark Scheme	$\frac{d^2 y}{d x^2}=e^x(\cos x-\sin x)-e^x(\sin x+\cos x)=-2 e^x \sin x$ Answer: B
Question Text	Consider the function $f$ defined by $f(x)=e^x \cos x,-\frac{\pi}{2} \leq x \leq \frac{\pi}{2}$ . (c) The function $f$ has a local maximum value when $x=\frac{\pi}{n}$ . Find the value of $n$ when $n \in Z^{+}$
Total Mark	2
Correct Answer	4
Explanation	na
Mark Scheme	$\begin{gathered} \frac{d y}{d x}=e^x(\cos x-\sin x)=0 \\ \cos x=\sin x \end{gathered}$ $x=\frac{\pi}{4}$ hence maximum at $x=\frac{\pi}{4}$ Answer: 4
Question Text	(d) Find the $x$ -coordinate of the point of inflextion of the graph $f(x)$
Total Mark	2
Correct Answer	0
Explanation	na
Mark Scheme	$\begin{gathered} \frac{d^2 y}{d x^2}=-2 e^x \sin x=0 \\ x=0 \end{gathered}$ Answer: 0
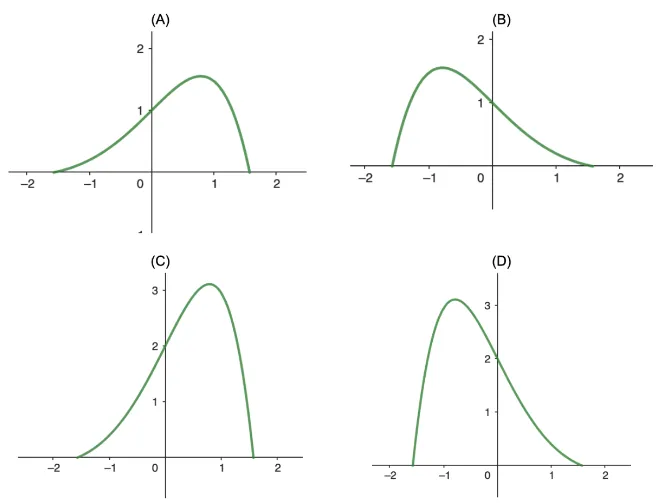
Question Text	(e) Sketch the graph of $f$ , clearly indicating the position of the local maximum point, the point of inflexion and the axes intercepts.

Total Mark	3
Correct Answer	a
Explanation	na
Mark Scheme	na
Question Text	(f) Find the area of the region enclosed by the graph of $f$ and the $x$ - axis. (a) $\frac{e^{-\pi / 2}}{2}$ (b) $\frac{e^{\pi / 2}}{2}$ (c) $\frac{e^\pi+e^{-\pi}}{2}$ (d) $\frac{e^{\pi / 2}+e^{-\pi / 2}}{2}$
Total Mark	6
Correct Answer	d
Explanation	na
Mark Scheme	Integration by parts $\begin{aligned} & \int_{-\pi / 2}^{\pi / 2} e^x \cos x d x=\left[e^x \cos x\right]{-\pi / 2}^{\pi / 2}+\int{-\pi / 2}^{\pi / 2} e^x \sin x d x \\ & =\left[e^x \cos x\right]{-\pi / 2}^{\pi / 2}+\left[e^x \sin x\right]{-\pi / 2}^{\pi / 2}-\int_{-\pi / 2}^{\pi / 2} e^x \cos x d x \end{aligned}$ Setting $I=\int_{-\pi / 2}^{\pi / 2} e^x \cos x d x$ , $\begin{gathered} I=\left[e^x \cos x\right]{-\pi / 2}^{\pi / 2}+\left[e^x \sin x\right]{-\pi / 2}^{\pi / 2}-I \\ 2 I=\left[e^x \cos x\right]{-\pi / 2}^{\pi / 2}+\left[e^x \sin x\right]{-\pi / 2}^{\pi / 2} \\ I=\frac{e^{\pi / 2}+e^{-\pi / 2}}{2} \end{gathered}$ Answer: D

Topic	5.5 Applications of integration
Tag	Integration Area Inverse Function Area Between Two Functions Solids of Revolution Kinematics Trigonometric Functions Logarithmic Functions Intercepts By Parts Substitution Partial Fractions Related Rates
Source	M16-TZ2-P1-11(HL)
Question Text	The graph of $x=2 \sin 2 y+3,0 \leq y \leq \pi$ is rotated 360 degrees about the $y$ -axis to form a volume of revolution. (a) The volume generated can be written in the form $a \pi^2$ where $a \in Z^{+}$ . Find the value of $a$ .
Total Mark	8
Correct Answer	11
Explanation	na
Mark Scheme	use of $\pi \int_a^b x^2 d y$ $\begin{gathered} V=\pi \int_0^\pi(2 \sin 2 y+3)^2 d y \\ =\pi \int_0^\pi\left(4 \sin ^2 2 y+12 \sin 2 y+9\right) d y \end{gathered}$ As $4 \sin ^2 2 y=2(1-\cos 4 y)$ $\begin{aligned} & =\pi \int_0^\pi(12 \sin 2 y-2 \cos 4 y+11) d y \\ & =\pi\left[-6 \cos 2 y-\frac{1}{2} \sin 4 y+11 y\right]_0^\pi \\ & =\pi(-6+11 \pi+6)=11 \pi^2 \end{aligned}$ Answer: 11
Question Text	(b) A container with this shape is made with a solid base of diameter 6 cm . The container is filled with water a $t$ a rate of $1 \mathrm{~cm}^3 \mathrm{~min}^{-1}$ . At time $t$ minutes, the water depth is $h \mathrm{~cm}, 0 \leq h \leq \pi$ and the volume of water in the container $V \mathrm{~cm}^3$ . (i) Given that $\frac{d V}{d h}=\pi(2 \sin 2 h+3)^2$ , find an expression for $\frac{d h}{d t}$ . (a) $\frac{d h}{d t}=\frac{1}{\pi(2 \cos 2 h+3)^2}$ (b) $\frac{d h}{d t}=\frac{1}{\pi(2 \sin 2 h+3)^2}$ (c) $\frac{d h}{d t}=\pi(2 \cos 2 h+3)^2$ (d) $\frac{d h}{d t}=\pi(2 \sin 2 h+3)^2$ Total Mark : 3 Correct Answer : b Explanation : na Mark Scheme : use $\frac{d h}{d t}=\frac{d V}{d t} \times \frac{d h}{d V}$ with $\frac{d V}{d t}=1$ $\frac{d h}{d t}=\frac{1}{\pi(2 \sin 2 h+3)^2}$ Answer: B (ii) The value of $\frac{d h}{d t}$ when $h=\frac{\pi}{4}$ can be written as $\frac{1}{n \pi}$ where $n \in Z^{+}$ . Find the value of $n$ . Total Mark : 4 Correct Answer : 25 Explanation : na Mark Scheme : substituting $h=\frac{\pi}{4}$ into $\frac{d h}{d t}$ $\frac{d h}{d t}=\frac{1}{\pi\left(2 \sin \left(\frac{\pi}{4}\right)+3\right)^2}=\frac{1}{25 \pi}$ Answer: 25
Question Text	(c) (i) Find $\frac{d^2 h}{d t^2}$ . Total Mark : ? Correct Answer : $\frac{-8 \cos 2 h}{\pi^2(2 \cos 2 h+3)^5}$ Explanation : na Mark Scheme : $\frac{d^2 h}{d t^2}=\frac{d}{d t}\left(\frac{d h}{d t}\right)=\frac{d h}{d t} \times \frac{d}{d h}\left(\frac{d h}{d t}\right)$ $\begin{gathered} =\frac{1}{\pi(2 \sin 2 h+3)^2} \times \frac{-2 \times 4 \cos 2 h}{\pi(2 \sin 2 h+3)^3} \\ =\frac{-8 \cos 2 h}{\pi^2(2 \cos 2 h+3)^5} \end{gathered}$ (ii) Select all the values of $h$ for which $\frac{d^2 h}{d t^2}=0$ (select all that apply) (a) 0 (b) $\frac{\pi}{4}$ (c) $\frac{\pi}{2}$ (d) $\frac{3 \pi}{4}$ (e) $\pi$ Total Mark : 5 Correct Answer : b,d Explanation : na Mark Scheme : $\begin{aligned} & \cos 2 h=0 \\ & h=\frac{\pi}{4}, \frac{3 \pi}{4} \end{aligned}$ Answer: B, D

Topic	5.5 Applications of integration
Tag	Integration Area Inverse Function Area Between Two Functions Solids of Revolution Kinematics Trigonometric Functions Logarithmic Functions Intercepts By Parts Substitution Partial Fractions Related Rates
Source	M15-TZ2-P1-11(HL)
Question Text	Consider the functions $f(x)=\tan x, 0 \leq x<\frac{\pi}{2}$ and $g(x)=\frac{x-1}{x+1}, x \in R, x \neq 1$ . (a) Find the correct expression for $g \circ f(x)$ [multiple choice] (a) $g \circ f(x)=\frac{\tan x+1}{\tan x-1}$ (b) $g \circ f(x)=\frac{\sin x-\cos x}{\sin x+\cos x}$ (c) $g \circ f(x)=\frac{\sin x+\cos x}{\sin x-\cos x}$ (d) $g \circ f(x)=\frac{\sin x}{\cos x}$
Total Mark	2
Correct Answer	b
Explanation	na
Mark Scheme	$\begin{gathered} g \circ f(x)=\frac{\tan x-1}{\tan x+1} \\ \frac{\tan x+1}{\tan x-1}=\frac{\frac{\sin x}{\cos x}-1}{\frac{\sin x}{\cos x}+1}=\frac{\sin x-\cos x}{\sin x+\cos x} \end{gathered}$ Answer: B
Question Text	(b) Find the area bounded by the graph of $y=g \circ f(x)$ , the $x$ -axis and the lines $x=0$ and $x=\frac{\pi}{6}$ . (a) $\sqrt{3}+1$ (b) $\ln (\sqrt{3}+1)$ (c) $\sqrt{3}-1$ (d) $\ln (\sqrt{3}-1)$
Total Mark	6
Correct Answer	d
Explanation	na
Mark Scheme	$\begin{aligned} & \text { Area }=\left\|\int_0^{\frac{\pi}{6}} \frac{\sin x-\cos x}{\sin x+\cos x} d x\right\| \\ & =\left\|[-\ln \|\sin x+\cos x\|]_0^{\frac{\pi}{6}}\right\| \\ & \left.=\|-\ln \| \sin \frac{\pi}{6}+\cos \frac{\pi}{6}\|+\ln \| \sin 0+\cos 0 \right\rvert\, \\ & =-\ln \left\|\frac{1}{2}+\frac{\sqrt{3}}{2}\right\|=\ln \frac{2}{\sqrt{3}+1}=\ln (\sqrt{3}-1) \end{aligned}$ Answer: D

Topic	5.5 Applications of integration
Tag	Integration Area Inverse Function Area Between Two Functions Solids of Revolution Kinematics Trigonometric Functions Logarithmic Functions Intercepts By Parts Substitution Partial Fractions Related Rates
Source	N13-TZ0-P1-12(HL)
Question Text	Consider the complex number $z=\cos \theta-i \sin \theta$ . (a) The value of $16 \cos ^4 \theta$ can be written as $a \cos 4 \theta+b \cos 2 \theta+c, a, b, c \in Z^{+}$ . By considering $\left(z+z^{-1}\right)^4$ , find the value of $a+b+c$
Total Mark	5
Correct Answer	16
Explanation	na
Mark Scheme	$\left(z+z^{-1}\right)^4=z^4+4 z^3\left(\frac{1}{z}\right)+6 z^2\left(\frac{1}{z^2}\right)+4 z\left(\frac{1}{z^3}\right)+\frac{1}{z^4} \\ \left(z+z^{-1}\right)^4=\left(z^4+\frac{1}{z^4}\right)+4\left(z^2+\frac{1}{z^2}\right)+6 \\$ As $z=\cos (-\theta)+i \sin (-\theta)$ $\quad(2 \cos (-\theta))^4=2 \cos 4 \theta+8 \cos 2 \theta+6$ Answer: 16
Question Text	(b) Hence find the value of $\int_0^{\frac{\pi}{2}} \cos ^4 \theta d \theta$ . (a) $\frac{3\pi }{16}$ (b) $\frac{5\pi }{16}$ (c) $\frac{\pi }{4}$ (d) $\frac{\pi }{16}$
Total Mark	3
Correct Answer	a
Explanation	na
Mark Scheme	$\begin{aligned} & \int_0^{\frac{\pi}{2}} \cos ^4 \theta d \theta=\int_0^{\frac{\pi}{2}}\left(\frac{1}{8} \cos 4 \theta+\frac{1}{2} \cos 2 \theta+\frac{3}{8}\right) d \theta \\ & \quad=\left[\frac{1}{32} \sin 4 \theta+\frac{1}{4} \sin 2 \theta+\frac{3}{8} \theta\right]_0^{\frac{\pi}{2}}=\frac{3 \pi}{16}\end{aligned}$
Question Text	(c) (i) Write down an expression for the constant term in the expansion of $\left(z+z^{-1}\right)^6, k \in Z^{+}$ . Total Mark : 4 Correct Answer : 20 Explanation : na Mark Scheme : constant term = $\frac{6!}{3!3!}=20$ Answer: 20 (ii) Hence, if $\int_0^{\frac{\pi}{2}} \cos ^6 \theta d \theta$ can be written as $\frac{a \pi}{b}$ where $a, b$ are positive integers in lowest terms, find the value of $a+b$ . Total Mark : 5 Correct Answer : 37 Explanation : na Mark Scheme : Considering the answer found in part (b), all other terms except for the constant term is equal to 0. $\begin{aligned} & 2 \int_0^{\frac{\pi}{2}} \cos ^6 \theta d \theta=[20 \times \theta]_0^{\frac{\pi}{2}} \\ & \int_0^{\frac{\pi}{2}} \cos ^6 \theta d \theta=\frac{10 \pi}{64}=\frac{5 \pi}{32} \end{aligned}$ Answer: 37
Question Text	(d) The graph of $f(x)=\sin x \cos ^2 x 0 \leq x \leq \frac{\pi}{2}$ is rotated by around the $x$ -axis. The volume of this solid can be written as $\frac{a \pi^2}{b}$ where $a, b$ are positive integers in lowest terms. Find the value of $a+b$ .
Total Mark	6
Correct Answer	33
Explanation	na
Mark Scheme	$V=\pi \int_0^{\frac{\pi}{2}} \sin ^2 x \cos ^4 x d x$ Using $\sin ^2 x=1-\cos ^2 x$ $\pi \int_0^{\frac{\pi}{2}} \cos ^4 x d x-\pi \int_0^{\frac{\pi}{2}} \cos ^6 x d x=\frac{3 \pi^2}{16}-\frac{5 \pi^2}{32}=\frac{\pi^2}{32}$ Answer: 33

Topic	5.5 Applications of integration
Tag	Integration Area Inverse Function Area Between Two Functions Solids of Revolution Kinematics Trigonometric Functions Logarithmic Functions Intercepts By Parts Substitution Partial Fractions Related Rates
Source	N19/5/MATHL/HP1/ENG/TZ1/XX/10d
Question Text	Consider $f(x)=\frac{2 x-3}{x^2-1}$ (a) The value of $\frac{2 x-3}{x^2-1}$ can be written as $\frac{B}{x+1}-\frac{A}{x-1}$ where $B$ is a prime number. Find the value of $A+B$ .
Total Mark	4
Correct Answer	3
Explanation	n/a
Mark Scheme	$\begin{gathered} \frac{B}{x+1}-\frac{A}{x-1}=\frac{B(x-1)-A(x+1)}{x^2-1} \\ \frac{(B-A) x-A-B}{x^2-1}=\frac{2 x-3}{x^2-1} \end{gathered}$ $A=\frac{1}{2}, B=\frac{5}{2}$ Answer: 3
Question Text	(b) The value of $2 \int_0^{\frac{1}{2}} f(x) d x$ can be written as $\ln \frac{a}{b}$ where $a, b$ are positive integers in lowest terms FInd the value of $a+b$ .
Total Mark	7
Correct Answer	259
Explanation	n/a
Mark Scheme	$\begin{gathered} 2 \int_0^{\frac{1}{2}} f(x) d x=\int_0^{\frac{1}{2}} \frac{5}{x+1}-\frac{1}{x-1} d \\ =[5 \ln \|x+1\|-\ln \|x-1\|]_0^{\frac{1}{2}} \\ =\left(5 \ln \frac{3}{2}-\ln \frac{1}{2}-(5 \ln 1-\ln 1)\right) \\ =\ln \frac{3^5}{2^4} \\ =\ln \frac{243}{16} \end{gathered}$ Answer: 259

Topic	5.5 Applications of integration
Tag
Source	M19/5/MATHL/HP1/ENG/TZ2/XX/9
Question Text	Consider the functions $f$ and $g$ defined on the domain $0<x<2 \pi$ by $f(x)=2 \cos 2 x$ and $g(x)=1-5 \cos x$ . (a) Select the all possible $x$ - coordinates of the points of intersection of the two graphs. (select all that apply) (a) $\frac{\pi}{3}$ (b) $\frac{2 \pi}{3}$ (c) $\pi$ (d) $\frac{4 \pi}{3}$ (e) $\frac{5 \pi}{3}$
Total Mark	6
Correct Answer	a,e
Explanation	n/a
Mark Scheme	$3 \cos 2 x=1-5 \cos x$ Use of $\cos 2 x=2 \cos ^2 x-1$ $\begin{gathered} 3\left(2 \cos ^2 x-1\right)=1-5 \cos x \\ 6 \cos ^2 x+3 \cos x-4=0 \\ (2 \cos x-1)(3 \cos x+4)=0 \\ \cos x=\frac{1}{2} \\ x=\frac{\pi}{3}, \frac{5 \pi}{3} \end{gathered}$ Answer: (A), (E)
Question Text	(b) Find the area enclosed by the two graphs. [multiple choice] (a) $\frac{4 \pi}{3}+5 \sqrt{3}$ (b) $\frac{2 \pi}{3}+4 \sqrt{3}$ (c) $\frac{\pi}{3}+3 \sqrt{3}$ (d) $\frac{\pi}{3}+2 \sqrt{3}$
Total Mark	3
Correct Answer	a
Explanation	n/a
Mark Scheme	$\begin{gathered} \left\|\int_{\frac{\pi}{3}}^{\frac{5 \pi}{3}}(1-5 \cos x-3 \cos 2 x) d x\right\| \\ =\left\|\left[x-5 \sin x-\frac{3}{2} \sin 2 x\right]_{\frac{\pi}{3}}^{\frac{5 \pi}{3}}\right\| \\ =\left\|\frac{5 \pi}{3}+5 \frac{\sqrt{3}}{2}-\frac{3}{2} \times \frac{\sqrt{3}}{2}-\left(\frac{\pi}{3}-5 \frac{\sqrt{3}}{2}-\frac{3}{2} \times \frac{\sqrt{3}}{2}\right)\right\| \\ =\left\|\frac{4 \pi}{3}+5 \sqrt{3}\right\|=\frac{4 \pi}{3}+5 \sqrt{3} \end{gathered}$ Answer: (A)

Topic	5.5 Applications of integration
Tag
Source	N18/5/MATHL/HP1/ENG/TZ0/XX/10
Question Text	(a) Use integration by parts tofind the value of $\int e^x \sin 2 x d x$ . [multiple choice] (a) $\frac{e^x}{5} \sin 2 x+\frac{e^x}{5} \cos 2 x+c$ (b) $\frac{3 e^x}{5} \sin 2 x-\frac{2 e^x}{5} \cos 2 x+c$ (c) $\frac{4 e^x}{5} \sin 2 x+\frac{3 e^x}{5} \cos 2 x+c$ (d) $\frac{e^x}{5} \sin 2 x-\frac{2 e^x}{5} \cos 2 x+c$
Total Mark	5
Correct Answer	d
Explanation	n/a
Mark Scheme	Attempt at integration by parts with $u=e^x, \frac{d v}{d x}=\sin 2 x$ $\begin{aligned} & \int e^x \sin 2 x d x=-\frac{e^x}{2} \cos 2 x d x+\int \frac{e^x}{2} \cos 2 x d x \\ & =-\frac{e^x}{2} \cos 2 x+\frac{1}{2}\left(\frac{e^x}{2} \sin 2 x-\int \frac{e^x}{2} \sin 2 x\right) \end{aligned}$ Rearranging, $\begin{aligned} & \frac{5}{4} \int e^x \sin 2 x d x=\frac{e^x}{4} \sin 2 x-\frac{e^x}{2} \cos 2 x+c \\ & \int e^x \sin 2 x d x=\frac{e^x}{5} \sin 2 x-\frac{2 e^x}{5} \cos 2 x+c \end{aligned}$ Answer: D
Question Text	(b) Hence, find the value of $\int e^x \cos x \sin x d x$ . (a) $\frac{e^x}{10} \sin 2 x+\frac{e^x}{10} \cos 2 x+c$ (b) $\frac{3 e^x}{10} \sin 2 x-\frac{e^x}{5} \cos 2 x+c$ (c) $\frac{2 e^x}{5} \sin 2 x+\frac{3 e^x}{10} \cos 2 x+c$ (d) $\frac{e^x}{10} \sin 2 x-\frac{e^x}{5} \cos 2 x+c$
Total Mark	3
Correct Answer	d
Explanation	n/a
Mark Scheme	As $\sin 2 x=2 \sin x \cos x$ $\begin{gathered} \int e^x \sin x \cos x d x=\frac{1}{2} \int e^x \sin 2 x d x \\ \int e^x \sin x \cos x d x=\frac{e^x}{10} \sin 2 x-\frac{e^x}{5} \cos 2 x+c \end{gathered}$ Answer: D
Question Text	(c) Given $1 \leq x \leq \pi$ , find the $x$ -intercepts of $f(x)=e^x \cos x \sin x$ . (select all that apply) (a) $\frac{\pi}{6}$ (b) $\frac{\pi}{3}$ (c) $\frac{\pi}{2}$ (d) $\frac{5 \pi}{6}$ (e) $\pi$
Total Mark	3
Correct Answer	c,e
Explanation	n/a
Mark Scheme	$\begin{gathered} e^x \cos x \sin x=0 \\ \sin 2 x=0 \\ x=\frac{\pi}{2}, \pi \end{gathered}$ Answer: C, E
Question Text	(d) Find the area enclosed by the curve and the $x$ -axis between the two x-intercepts, as shaded on the diagram. [multiple choice] (a) $\frac{e^{\pi / 2}}{5}$ (b) $\frac{e^{\pi / 2}+e^{\pi / 3}}{5}$ (c) $\frac{e^\pi}{5}$ (d) $\frac{e^\pi+e^{\pi / 2}}{5}$
Total Mark	5
Correct Answer	d
Explanation	n/a
Mark Scheme	$\begin{gathered} \left\|\int_{\pi / 2}^\pi e^x \sin x \cos x d x\right\|=\left\|\left[\frac{e^x}{10} \sin 2 x-\frac{e^x}{5} \cos 2 x\right]_{\frac{\pi}{2}}^\pi\right\| \\ =\left\|-\frac{e^\pi}{5}-\left(\frac{e^{\pi / 2}}{5}\right)\right\|=\frac{e^\pi+e^{\pi / 2}}{5} \end{gathered}$ Answer: D

Topic	5.5 Applications of integration
Tag
Source	M18/5/MATHL/HP1/ENG/TZ2/XX/8
Question Text	(a) Use the substitution $u=e^x$ to find $\int \frac{1}{e^x+4 e^{-x}} d x$ . [multiple choice] (a) $\frac{1}{2} \arcsin \left(\frac{e^x}{2}\right)+c$ (b) $\frac{1}{2} \arctan \left(\frac{e^x}{2}\right)+c$ (c) $\arctan \left(e^x\right)+c$ (d) $\arcsin \left(e^x\right)+c$
Total Mark	4
Correct Answer	b
Explanation	na
Mark Scheme	$\begin{gathered} \frac{d u}{d x}=e^x \\ \int \frac{1}{u+4 u^{-1}} \times \frac{1}{u} d u \\ \int \frac{1}{u^2+4} d u=\frac{1}{2} \arctan \left(\frac{u}{2}\right)+c=\frac{1}{2} \arctan \left(\frac{e^x}{2}\right)+c \end{gathered}$ Answer: B
Question Text	(b) Hence, if the value of $2 \int_{\ln 2}^{\ln 2 \sqrt{3}} \frac{1}{e^x+4 e^{-x}} d x$ can expressed as $\frac{\pi}{n}$ , where $n \in Z$ , find the value of $n$
Total Mark	3
Correct Answer	6
Explanation	na
Mark Scheme	$\begin{aligned} & 2 \int_{\ln 2}^{\ln 2 \sqrt{3}} \frac{1}{e^x+4 e^{-x}} d x=\left[\arctan \left(\frac{e^x}{2}\right)\right]_{\ln 2}^{\ln 2 \sqrt{3}} \\ & =\arctan (\sqrt{3})-\arctan (1)=\frac{\pi}{3}-\frac{\pi}{2}=\frac{\pi}{6} \end{aligned}$ Answer: 6

5.5 Application of Integration

Q1

Q2

Q3

Q4

Q5

Q6

Q7

Q8

Q9

Q10