home
Mission
////////
home
////////

Matrices and Vectors

Tags

System of Equations

Many math IA topics frequently involve setting up and solving large systems of equations (see: extension from topic 1: “Systematic approaches to reliably obtain solutions to large systems of equations with mm equations and nn unknown variables (in the HL syllabus, we typically worked with m≤3m ≤ 3, n≤3n ≤ 3)” Managing complex (linear) systems of equations that have a large number of equations and unknown variables requires the use of simplifying notation and standardizing procedures

Augmented Matrices

a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋮⋮⋮am1x1+am2x2+⋯+amnxn=bm\begin{align*}a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n &= b_1 \\a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n &= b_2 \\\vdots \quad\quad \vdots \quad\quad &\vdots \\a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n &= b_m\end{align*}
[a11a12⋯a1nb1a21a22⋯a2nb2⋮⋮⋱⋮⋮am1am2⋯amnbm]\begin{bmatrix}a_{11} & a_{12} & \cdots & a_{1n} & b_1 \\a_{21} & a_{22} & \cdots & a_{2n} & b_2 \\\vdots & \vdots & \ddots & \vdots & \vdots \\a_{m1} & a_{m2} & \cdots & a_{mn} & b_m\end{bmatrix}

Elementary Row Operations

Three types of algebraic operations can be performed on equations to produce a succession of increasingly simpler systems that have the same solution set as the original system
1.
Multiply an equation through by a nonzero constant
2.
Interchange two equations
3.
Add a multiple of one equation to another

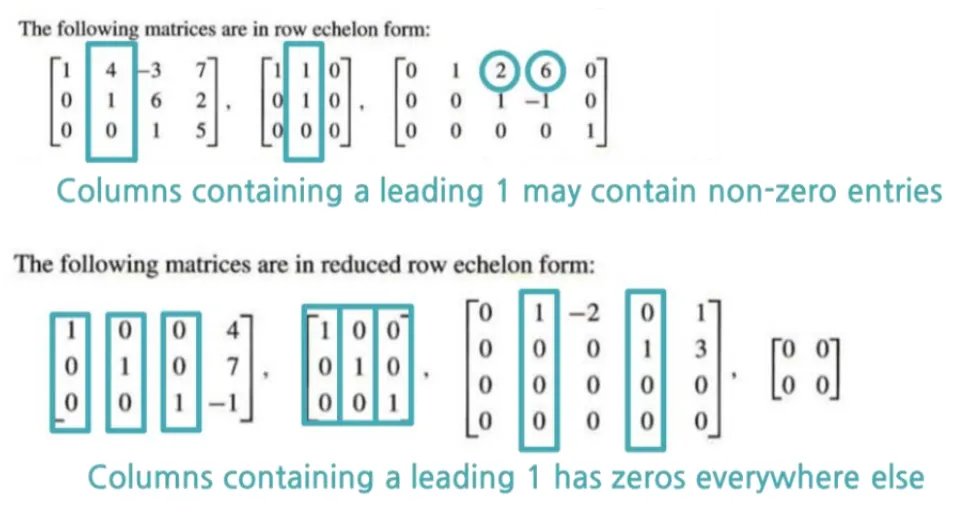
Reduced Row Echelon Form (RREF)

Reducing the augmented matrix into a RREF allows us to directly “read off” the solution

Gauss-Jordan Elimination

Gauss Elimination (Forward Phase): uses the three aforementioned elementary row operations to introduce zeros below the leading 1’s. Jordan Elimination (Backward Phase): uses the three aforementioned elementary row operations to introduce zeros above the leading 1’s.

Applications of Linear Systems of Equations

GPS Systems

Produce four equations with four unknown variables, (x, y, z and t). The coordinates of a satellite’s position at different times can be used to find the satellite’s position as a function of time.
Satellite
Satellite Position
Time
1
(1.12, 2.10, 1.40)
1.06
2
(0.00, 1.53, 2.30)
0.56
3
(1.40, 1.12, 2.10)
1.16
4
(2.30, 0.00, 1.53)
0.75
(x−x0)2+(y−y0)2+(z−z0)2=0.22(t−t0)2(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=0.22(t-t_0)^2

Network Analysis

Using the conservation of flow (water, charge, vehicles), elaborate pipe/circuit/road systems can be designed and analyzed.

Balancing Chemical Equations

Set up a system of equations where the coefficients of elements in a chemical reaction are represented as unknown variables.

Geometric Transformations Using Matrices (AI-friendly)

Transformation Matrices

Operator
Rotation about the positive x-axis through an angle θ
Rotation about the positive y-axis through an angle θ
Rotation about the positive z-axis through an angle θ
Illustration
Standard Matrix
[1000cos⁡θ−sin⁡θ0sin⁡θcos⁡θ]\begin{bmatrix}1 & 0 & 0 \\0 & \cos\theta & -\sin\theta \\0 & \sin\theta & \cos\theta\end{bmatrix}
[cos⁡θ0sin⁡θ010−sin⁡θ0cos⁡θ]\begin{bmatrix}\cos\theta & 0 & \sin\theta \\0 & 1 & 0 \\-\sin\theta & 0 & \cos\theta\end{bmatrix}
[cos⁡θ−sin⁡θ0sin⁡θcos⁡θ0001]\begin{bmatrix}\cos\theta & -\sin\theta & 0 \\\sin\theta & \cos\theta & 0 \\0 & 0 & 1\end{bmatrix}

Proof/ Derivation of Transformation Matrices

1.
Rotation about origin
2.
Reflection across line that makes an angle θ\theta with the xx-axis
3.
Orthogonal Projection onto a line

Composite Transformations

Rθ=[cos⁡θ−sin⁡θsin⁡θcos⁡θ]R_\theta=\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}
Rotation about the origin through an angle θ\theta
Hθ=[cos⁡2θsin⁡2θsin⁡2θ−cos⁡2θ]H_\theta=\begin{bmatrix} \cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \end{bmatrix}
Reflection about the line through the origin making an angle θ\theta with the positive xx-axis
Pθ=[cos⁡2θsin⁡θcos⁡θsin⁡θcos⁡θsin⁡2θ]P_\theta=\begin{bmatrix} \cos^2\theta & \sin\theta\cos\theta \\ \sin\theta\cos\theta & \sin^2\theta \end{bmatrix}
Orthogonal projection onto the line through the origin making an angle θ\theta with the positive xx-axis
The following theorem shows that the composition of two linear transformations is itself a linear transformation.
If T1:Rn→RkT_1:R^n\rightarrow R^k and T2:Rk→RmT_2:R^k\rightarrow R^m are both linear transformations, then (T2⋅T1):Rn→Rm(T_2\cdot T_1):R^n\rightarrow R^m is also a linear transformation,
Example 1: Composing Rotations in R2R^2
Let T1:R2→R2T_1:R^2\rightarrow R^2 be the rotation about the origion of R2R^2 through the angle θ1\theta_1, and let T2:R2→R2T_2:R^2\rightarrow R^2 be the rotation about the origin through the angle θ2\theta_2. The standard matrices for these rotations are
Rθ1=[cos⁡θ1−sin⁡θ1sin⁡θ1cos⁡θ1]R_{\theta_1}=\begin{bmatrix} \cos \theta_1 & -\sin\theta_1 \\ \sin\theta_1 & \cos\theta_1 \end{bmatrix} and Rθ2=[cos⁡θ2−sin⁡θ2sin⁡θ2cos⁡θ2]R_{\theta_2}=\begin{bmatrix} \cos \theta_2 & -\sin\theta_2 \\ \sin\theta_2 & \cos\theta_2 \end{bmatrix} (4)
The composition
(T2⋅T1)(x)=T2(T1(x))(T_2\cdot T_1)(x)=T_2(T_1(x))
first rotates xx through the angle θ1\theta_1 and then rotates T1(x)T_1(x) through the angle θ2\theta_2, so the standard matrix for T2⋅T1T_2\cdot T_1 should be
Rθ1+θ2=[cos⁡(θ1+θ2)−sin⁡(θ1+θ2)sin⁡(θ1+θ2)cos⁡(θ1+θ2)]R_{\theta_1+\theta_2}=\begin{bmatrix} \cos (\theta_1+\theta_2) & -\sin(\theta_1+\theta_2) \\ \sin(\theta_1+\theta_2) & \cos(\theta_1+\theta_2) \end{bmatrix} (5)
To confirm that this is so let us apply Formula (2). According to that formula the standard matrix T2⋅T1T_2\cdot T_1 is
Rθ2Rθ1=[cos⁡θ2−sin⁡θ2sin⁡θ2cos⁡θ2][cos⁡θ1−sin⁡θ1sin⁡θ1cos⁡θ1]R_{\theta_2}R_{\theta_1}=\begin{bmatrix} \cos \theta_2 & -\sin\theta_2 \\ \sin\theta_2 & \cos\theta_2 \end{bmatrix} \begin{bmatrix} \cos \theta_1 & -\sin\theta_1 \\ \sin\theta_1 & \cos\theta_1 \end{bmatrix}
=[cos⁡θ2cos⁡θ1−sin⁡θ2sin⁡θ1−cos⁡θ2sin⁡θ1−sin⁡θ2cos⁡θ1sin⁡θ2cos⁡θ1+cos⁡θ2sin⁡θ1−sin⁡θ2sin⁡θ1+cos⁡θ2cos⁡θ1]=\begin{bmatrix} \cos \theta_2\cos\theta_1-\sin\theta_2\sin\theta_1 & -\cos\theta_2\sin\theta_1-\sin\theta_2\cos\theta_1 \\ \sin\theta_2\cos\theta_1+\cos\theta_2\sin\theta_1 & -\sin\theta_2\sin\theta_1+\cos\theta_2\cos\theta_1 \end{bmatrix}
=[cos⁡(θ1+θ2)−sin⁡(θ1+θ2)sin⁡(θ1+θ2)cos⁡(θ1+θ2)]\begin{bmatrix} \cos (\theta_1+\theta_2) & -\sin(\theta_1+\theta_2) \\ \sin(\theta_1+\theta_2) & \cos(\theta_1+\theta_2) \end{bmatrix}
which agrees with (5).
Example 2: Composing Reflections
By Formula (18) of Section 6.1, the matrices
Hθ1=[cos⁡2θ1sin⁡2θ1sin⁡2θ1−cos⁡2θ1]H_{\theta_1}=\begin{bmatrix} \cos 2\theta_1 & \sin2\theta_1 \\ \sin2\theta_1 & -\cos2\theta_1 \end{bmatrix} and Hθ2=[cos⁡2θ2sin⁡2θ2sin⁡2θ2−cos⁡2θ2]H_{\theta_2}=\begin{bmatrix} \cos 2\theta_2 & \sin2\theta_2 \\ \sin2\theta_2 & -\cos2\theta_2 \end{bmatrix}
represent reflections about lines through the origin of R2R^2 making angles of θ1\theta_1 and θ2\theta_2 with the xx-axis, respectively. Accordingly, if we first reflect about the line making the angle θ1\theta_1 and then about the line making the angle θ2\theta_2, then we obtain a linear operator whose standard matrix is
Hθ2Hθ1=[cos⁡2θ2sin⁡2θ2sin⁡2θ2−cos⁡2θ2][cos⁡2θ1sin⁡2θ1sin⁡2θ1−cos⁡2θ1]H_{\theta_2}H_{\theta_1}=\begin{bmatrix} \cos2 \theta_2 & \sin2\theta_2 \\ \sin2\theta_2 & -\cos2\theta_2 \end{bmatrix} \begin{bmatrix} \cos 2\theta_1 & \sin2\theta_1 \\ \sin2\theta_1 & -\cos2\theta_1 \end{bmatrix}
=[cos⁡2θ2cos⁡2θ1+sin⁡2θ2sin⁡2θ1cos⁡2θ2sin⁡2θ1−sin⁡2θ2cos⁡2θ1sin⁡2θ2cos⁡2θ1−cos⁡2θ2sin⁡2θ1sin⁡2θ2sin⁡2θ1+cos⁡2θ2cos⁡2θ1]=\begin{bmatrix} \cos 2\theta_2\cos2\theta_1+\sin2\theta_2\sin2\theta_1 & \cos2\theta_2\sin2\theta_1-\sin2\theta_2\cos2\theta_1 \\ \sin2\theta_2\cos2\theta_1-\cos2\theta_2\sin2\theta_1 & \sin2\theta_2\sin2\theta_1+\cos2\theta_2\cos2\theta_1 \end{bmatrix}
=[cos⁡(2θ+2θ1)−sin⁡(2θ2+θ1)sin⁡(2θ2+2θ1)cos⁡(2θ2+2θ1)]=\begin{bmatrix} \cos (2\theta_+2\theta_1) & -\sin(2\theta_2+\theta_1) \\ \sin(2\theta_2+2\theta_1) & \cos(2\theta_2+2\theta_1) \end{bmatrix}
Comparing this matrix to the matrix RθR_\theta in formula (16) of Section 6.1, we see that this matrix represents a rotation about the origin through an angle of 2θ2−2θ12\theta_2-2\theta_1. Thus, we have shown that
Hθ2Hθ1=R2(θ2−θ1)H_{\theta_2}H_{\theta_1}=R_{2(\theta_2-\theta_1)}
This results is illustrated in Figure 6.4.2.