3.3 Trig functions and identities

Topic	3.3 Trig functions and identities
Tag	Trigonometry; Trigonometric functions; Sine; Cosine; Tangent; Triangle; Radians; Degrees; Period; Amplitude; Principal axis; Inverse; Trigonometric identities; Angle; Reciprocal
Source	M16-TZ1-P1-3(HL)
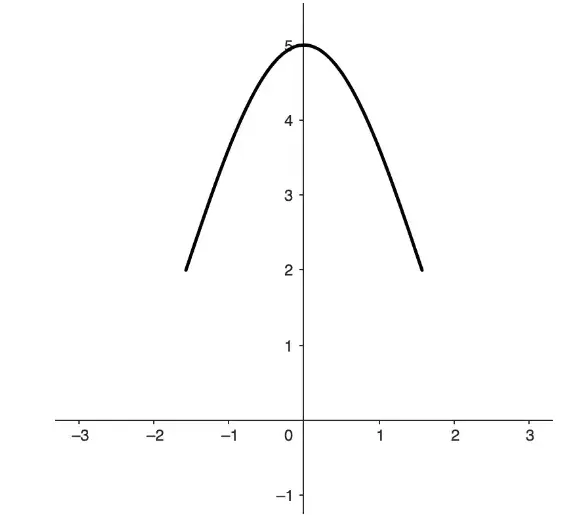
Question Text	The curve $y=a \sin (b(x-c))+d$ , where $a, b, c$ and $d$ are all positive constants. has a maximum point at $(1, 5)$ and a minimum point at $(2,1)$ . (a) Write down the value of $a$ .
Total Mark	1
Correct Answer	2
Explanation	na
Mark Scheme	(a) As the amptiltude is 2 $a=2$ Answer: 2
Question Text	(b) Write down the value of $d$
Total Mark	1
Correct Answer	3
Explanation	na
Mark Scheme	The center $y$ -coordinate is, $\frac{5+1}{2}=3$ Answer: 3
Question Text	(c) Find the value of $b$ . (a) 1 (b) 2 (c) $\pi$ (d) $2 \pi$
Total Mark	2
Correct Answer	c
Explanation	na
Mark Scheme	The period is 2 $b=\frac{2 \pi}{2}=\pi$ Answer: C
Question Text	(d) Find the smallest value of $c$ , given $c>0$ . (a) 0.5 (b) 1 (c) 1.5 (d) 2
Total Mark	2
Correct Answer	a
Explanation	na
Mark Scheme	$y=0$ when $x=0.5,1.5,2.5$ etc As the a sine curve has $x=0, y=0$ , the smallest value of $c$ is 0.5 (a rightward translation of 0.5 units) Answer: A

Topic	3.3 Trig functions and identities
Tag	Trigonometry; Trigonometric functions; Sine; Cosine; Tangent; Triangle; Radians; Degrees; Period; Amplitude; Principal axis; Inverse; Trigonometric identities; Angle; Reciprocal
Source	N16-TZ0-P1-9(HL)
Question Text	Solve the equation $\sin 2 x+\cos 2 x=1-\sin x+\cos x$ for $x \in[-\pi, \pi]$ (select all that apply). (a) $-\frac{3 \pi}{4}$ (b) $-\frac{\pi}{4}$ (c) $\frac{\pi}{6}$ (d) $\frac{\pi}{4}$ (e) $\frac{5 \pi}{6}$
Total Mark	7
Correct Answer	a,c,d,e
Explanation	na
Mark Scheme	Using the double angle formula $2 \sin x \cos x+\cos ^2 x-\sin ^2 x+\sin x-\cos x-1=0$ As $\cos ^2 x+\sin ^2 x=1$ $\begin{gathered} 2 \sin x \cos x-2 \sin ^2 x+\sin x-\cos x=0 \\ (2 \sin x-1)(\cos x-\sin x)=0 \end{gathered}$ So either $\begin{aligned} & 2 \sin x-1=0 \text { or } \cos x=\sin x \\ & x=-\frac{3 \pi}{4}, \frac{\pi}{6}, \frac{\pi}{4}, \frac{5 \pi}{6} \end{aligned}$ Answer: A, C, D, E

Topic	3.3 Trig functions and identities
Tag	Trigonometry; Trigonometric functions; Sine; Cosine; Tangent; Triangle; Radians; Degrees; Period; Amplitude; Principal axis; Inverse; Trigonometric identities; Angle; Reciprocal
Source	M15-TZ2-P1-3(HL)
Question Text	Find all solutions to the equation $\tan 2 x-\tan x=0$ where $0^{\circ} \leq x<180^{\circ}$ . (select all that apply) (a) 0 (b) 45 (c) 90 (d) 120 (e) 180
Total Mark	6
Correct Answer	a,b,e
Explanation	na
Mark Scheme	$\begin{gathered} \tan 2 x-\tan x=0 \\ \frac{2 \tan x}{1-\tan ^2 x}-\tan x=0 \\ \tan ^2 x-\tan x=\tan x(\tan x-1)=0 \\ \tan x=0 \text { or } \tan x-1=0 \end{gathered}$ So $x=0,45,180$ Answer: A, B, E

Topic	3.3 Trig functions and identities
Tag	Trigonometry; Trigonometric functions; Sine; Cosine; Tangent; Triangle; Radians; Degrees; Period; Amplitude; Principal axis; Inverse; Trigonometric identities; Angle; Reciprocal
Source	N14/5/MATHL/HP1/ENG/TZ0/XX/13b
Question Text	Use the double angle identity $\tan 2 \theta=\frac{2 \tan \theta}{1-\tan ^2 \theta}$ to find the expression for $\tan \frac{3 \pi}{8}$ (a) $1+\sqrt{2}$ (b) $\sqrt{2}-1$ (c) $\frac{1+\sqrt{2}}{2}$ (d) $\frac{\sqrt{2}-1}{2}$
Total Mark	4
Correct Answer	a
Explanation	na
Mark Scheme	$\begin{gathered} \tan \frac{3 \pi}{4}=\frac{2 \tan \frac{3 \pi}{8}}{1-\tan ^2 \frac{3 \pi}{8}} \\ \tan ^2 \frac{3 \pi}{8}-2 \tan \frac{3 \pi}{8}-1=0 \end{gathered}$ $\text { let } A=\tan \frac{3 \pi}{8}$ Solve $A^2-2 A-1=0$ $A=1 \pm \sqrt{2}$ $\frac{3 \pi}{8}$ is a first quadrant angle and tan is positive in this quadrant, so $\tan \frac{\pi}{8}>0$ $\tan \frac{3 \pi}{8}=1+\sqrt{2}$ Answer: A

Topic	3.3 Trig functions and identities
Tag	Trigonometry; Trigonometric functions; Sine; Cosine; Tangent; Triangle; Radians; Degrees; Period; Amplitude; Principal axis; Inverse; Trigonometric identities; Angle; Reciprocal
Source	M14/5/MATHL/HP1/ENG/TZ1/X/5
Question Text	(a) Use the identity $\cos 2 \theta=2 \cos ^2 \theta-1$ to find an expression for $\cos \frac{1}{2} x, 0 \leq x \leq \pi$ . (a) $-\sqrt{\frac{1+\cos x}{2}}$ (b) $-\sqrt{\frac{1-\cos x}{2}}$ (c) $\sqrt{\frac{1+\cos x}{2}}$ (d) $\sqrt{\frac{1-\cos x}{2}}$
Total Mark	3
Correct Answer	c
Explanation	na
Mark Scheme	$\cos x=2 \cos ^2 \frac{1}{2} x-1$ Rearrange $\cos \frac{1}{2} x= \pm \sqrt{\frac{1+\cos x}{2}}$ $\cos \frac{1}{2} x$ is positive as $0 \leq x \leq \pi$ $\cos \frac{1}{2} x=\sqrt{\frac{1+\cos x}{2}}$ Answer: C
Question Text	(b) Find a similar expression for $\sin \frac{1}{2} x, 0 \leq x \leq \pi$ . (a) $-\sqrt{\frac{1+\cos x}{2}}$ (b) $-\sqrt{\frac{1-\cos x}{2}}$ (c) $\sqrt{\frac{1+\cos x}{2}}$ (d) $\sqrt{\frac{1-\cos x}{2}}$
Total Mark	2
Correct Answer	d
Explanation	na
Mark Scheme	$\begin{gathered} \cos 2 \theta=1-2 \sin ^2 \theta \\ \cos x=1-2 \sin ^2 \frac{1}{2} x \\ \sin \frac{1}{2} x=\sqrt{\frac{1-\cos x}{2}} \end{gathered}$ Answer: D

Topic	3.3 Trig functions and identities
Tag	Trigonometry; Trigonometric functions; Sine; Cosine; Tangent; Triangle; Radians; Degrees; Period; Amplitude; Principal axis; Inverse; Trigonometric identities; Angle; Reciprocal
Source	M14/5/MATHL/HP1/ENG/TZ1/X/10
Question Text	The value of $\sin 4 x$ can be expressed in the form $-\frac{a \sqrt{p}}{b}$ where $a, b$ are positive integers in lowest terms and $p$ is a prime number. Give than $\sin x+\cos x=\frac{1}{2}$ find the value of $a+b+p$
Total Mark	6
Correct Answer	18
Explanation	na
Mark Scheme	$\begin{gathered} \sin x+\cos x=\frac{1}{2} \\ (\sin x+\cos x)^2=\left(\frac{1}{2}\right)^2 \\ \sin ^2 x+2 \sin x \cos x+\cos ^2 x=\frac{1}{4} \end{gathered}$ Using $2 \sin x \cos x=\sin 2 x$ and $\sin ^2 x+\cos ^2 x=1$ $\sin 2 x=-\frac{3}{4}$ As $\sin 4 x=2 \sin 2 x \cos 2 x$ , in order to find $\cos 2 x$ $\begin{gathered} \sin ^2 2 x+\cos ^2 2 x=1 \\ \cos ^2 2 x=\frac{7}{16} \\ \cos 2 x=\frac{\sqrt{7}}{4} \end{gathered}$ So $\begin{gathered} \sin 4 x=2 \sin 2 x \cos 2 x=2 \times\left(-\frac{3}{4}\right) \times \frac{\sqrt{7}}{4} \\ \sin 4 x=-\frac{3 \sqrt{7}}{8} \end{gathered}$ Answer: 18

Topic	3.3 Trig functions and identities
Tag	Trigonometry; Trigonometric functions; Sine; Cosine; Tangent; Triangle; Radians; Degrees; Period; Amplitude; Principal axis; Inverse; Trigonometric identities; Angle; Reciprocal
Source
Question Text	Solve $y=\left\|\cos \frac{x}{2}\right\|=\frac{\sqrt{3}}{2}$ for $0 \leq x \leq 4 \pi$ (select all that apply). (a) $\frac{\pi}{3}$ (b) $\frac{2 \pi}{3}$ (c) $\frac{5 \pi}{3}$ (d) $\frac{7 \pi}{3}$ (e) $\frac{11 \pi}{3}$
Total Mark	3
Correct Answer	a,c,d,e
Explanation	na
Mark Scheme	$\begin{gathered} \left\|\cos \frac{x}{4}\right\|=\frac{\sqrt{3}}{2} \\ \cos \frac{x}{2}=\frac{\sqrt{3}}{2} \text { or }-\frac{\sqrt{3}}{2} \\ \frac{x}{2}=\frac{\pi}{6}, \frac{5 \pi}{6}, \frac{7 \pi}{6}, \frac{11 \pi}{6} \\ x=\frac{\pi}{3}, \frac{5 \pi}{3}, \frac{7 \pi}{3}, \frac{11 \pi}{3} \end{gathered}$ Answer: A, C, D, E

Topic	3.3 Trig functions and identities
Tag	Trigonometry; Trigonometric functions; Sine; Cosine; Tangent; Triangle; Radians; Degrees; Period; Amplitude; Principal axis; Inverse; Trigonometric identities; Angle; Reciprocal
Source	N13-TZ0-P1-8(HL)
Question Text	(a) Find an expression for $\cos (x+y) \cos (x-y)$ (a) $\cos ^2 x-\sin ^2 y$ (b) $\sin ^2 x-\sin ^2 y$ (c) $\cos ^2 x-\cos ^2 y$ (d) $\sin ^2 x-\cos ^2 y$
Total Mark	4
Correct Answer	a
Explanation	na
Mark Scheme	$\cos (x+y) \cos (x-y)=(\cos x \cos y-\sin x \sin y)(\cos x \cos y+\sin x \sin y)$ Utilizing the pythagorean identity $\begin{gathered} \cos ^2 x \cos ^2 y-\sin ^2 x \sin ^2 y=\cos ^2 x \cos ^2 y-\left(1-\cos ^2 x\right)\left(1-\cos ^2 y\right) \\ \cos ^2 x+\cos ^2 y-1=\cos ^2 x-\sin ^2 y \end{gathered}$ Answer: A
Question Text	(b) Given $f(x)=\cos \left(x+\frac{\pi}{6}\right) \cos \left(x-\frac{\pi}{6}\right), x \in[0, \pi]$ , find the range of $f$ . (a) $[0, \pi]$ (b) $\left[-\frac{\pi}{6}, \frac{5 \pi}{6}\right]$ (c) $\left[-\frac{3}{4}, \frac{1}{4}\right]$ (d) $\left[-\frac{1}{4}, \frac{3}{4}\right]$
Total Mark	2
Correct Answer	d
Explanation	na
Mark Scheme	$f(x)=\cos ^2 x-\sin ^2\left(\frac{\pi}{6}\right)=\cos ^2 x-\frac{1}{4}$ Answer: D range is $f \in\left[-\frac{1}{4}, \frac{3}{4}\right]$

Topic	3.3 Trig functions and identities
Tag	Trigonometry; Trigonometric functions; Sine; Cosine; Tangent; Triangle; Radians; Degrees; Period; Amplitude; Principal axis; Inverse; Trigonometric identities; Angle; Reciprocal
Source	M13-TZ1-P1-11(HL)
Question Text	(a) Consider the value of $\sin \left(\frac{\pi}{6}+x\right)$ . If the solution of $\cos x+\sqrt{3} \sin x=1$ for $0 \leq x \leq \frac{\pi}{2}$ can be written as $\frac{a \pi}{b}$ where $a$ and $b$ are positive integers in lowest terms. Find the value of $a+b$ .
Total Mark	7
Correct Answer	4
Explanation	na
Mark Scheme	$\begin{aligned} & \sin \left(\frac{\pi}{6}+x\right)=\sin \left(\frac{\pi}{6}\right) \cos x+\cos \left(\frac{\pi}{6}\right) \sin x \\ & \frac{1}{2} \cos x+\frac{\sqrt{3}}{2} \sin x=\frac{1}{2}(\cos x+\sqrt{3} \sin x) \end{aligned}$ Therefore, $\begin{gathered} \sin \left(\frac{\pi}{6}+x\right)=\frac{1}{2} \\ x=\frac{\pi}{3} \end{gathered}$ Answer: 4
Question Text	(b) Given that $\sin 2 \theta \sin \theta+3 \cos ^2 \theta=3$ for $0 \leq \theta \leq 2 \pi$ , by using the substitution $\cos \theta=x$ , find all solutions of the value of $x$ . (select all the apply). (a) -1 (b) 1 (c) $\frac{1}{2}$ (d) $-\frac{\sqrt{6}}{2}$ (e) $\frac{\sqrt{6}}{2}$
Total Mark	5
Correct Answer	b,d,e
Explanation	na
Mark Scheme	$\begin{gathered} 2 \sin \theta \cos \theta \sin \theta+\sin ^2 \theta=2 \cos \theta\left(1-\cos ^2 \theta\right)+3 \cos ^2 \theta \\ 2 \cos \theta-2 \cos ^3 \theta+3 \cos ^2 \theta=3 \\ 2 \cos ^3 \theta-2 \cos ^2 \theta-3 \cos \theta+3=0 \end{gathered}$ $2 x^3-2 x^2-3 x+3=0$ Noticing that $x=1$ is a valid solution, $(x-1)(2 x^2-3)$ Thus, $x=1, \frac{\sqrt{6}}{2},-\frac{\sqrt{6}}{2}$ Answer: B, D, E

Topic	3.3 Trig functions and identities
Tag	Trigonometry; Trigonometric functions; Sine; Cosine; Tangent; Triangle; Radians; Degrees; Period; Amplitude; Principal axis; Inverse; Trigonometric identities; Angle; Reciprocal
Source	M13-TZ2-P1-10(HL)
Question Text	(a) Given that $\arctan \left(\frac{1}{7}\right)-\arctan \left(\frac{1}{9}\right)=\arctan \left(\frac{1}{p}\right)$ , where $p \in Z^{+}$ , find $p$ .
Total Mark	3
Correct Answer	31
Explanation	na
Mark Scheme	Use of $\tan (A-B)=\frac{\tan (A)-\tan (B)}{1+\tan (A) \tan (B)}$ $\frac{1}{p}=\frac{\frac{1}{7}-\frac{1}{9}}{1-\frac{1}{7} \times \frac{1}{9}}=\frac{2 / 63}{62 / 63}=\frac{1}{31}$ Answer: 31
Question Text	(b) Hence given that $\arctan \left(\frac{1}{7}\right)+\arctan \left(\frac{1}{8}\right)-\arctan \left(\frac{1}{9}\right)=\arctan \left(\frac{a}{b}\right)$ where a and b are positive integers in lowest terms, find the value of $a+b$
Total Mark	3
Correct Answer	22
Explanation	na
Mark Scheme	Use of $\tan (A+B)=\frac{\tan (A)+\tan (B)}{1-\tan (A) \tan (B)}$ $\begin{gathered} \arctan \left(\frac{1}{7}\right)+\arctan \left(\frac{1}{8}\right)-\arctan \left(\frac{1}{9}\right)=\arctan \left(\frac{1}{31}\right)+\arctan \left(\frac{1}{8}\right) \\ \frac{\frac{1}{31}+\frac{1}{8}}{1-\frac{1}{31} \times \frac{1}{8}}=\frac{39 / 248}{247 / 248}=\frac{3}{19} \end{gathered}$ Answer: 22

Topic	3.3 Trig functions and identities
Tag	Trigonometry; Trigonometric functions; Sine; Cosine; Tangent; Triangle; Radians; Degrees; Period; Amplitude; Principal axis; Inverse; Trigonometric identities; Angle; Reciprocal
Source	M19/5/MATHL/HP1/ENG/TZ1/XX/9
Question Text	Find an expression for $\csc 2 x+\cot 2 x$ . (a) $\cot x$ (b) $\frac{1}{\sin x+\cos x}$ (c) $\frac{\sin x+\cos x}{\sin x-\cos x}$ (d) $\frac{\sin x-\cos x}{\sin x+\cos x}$
Total Mark	4
Correct Answer	a
Explanation	na
Mark Scheme	$\csc 2 x+\cot 2 x=\frac{1}{\sin 2 x}+\frac{\cos 2 x}{\sin 2 x}=\frac{1+\cos 2 x}{\sin 2 x}$ Using the double angle identities $\frac{1+\cos 2 x}{\sin 2 x}=\frac{2 \cos ^2 x}{2 \sin x \cos x}=\frac{\cos x}{\sin x}=\cot x$ Answer: A

Topic	3.3 Trig functions and identities
Tag	Trigonometry; Trigonometric functions; Sine; Cosine; Tangent; Triangle; Radians; Degrees; Period; Amplitude; Principal axis; Inverse; Trigonometric identities; Angle; Reciprocal
Source	N18/5/MATHL/HP1/ENG/TZ0/XX/3
Question Text	Consider the function $g(x)=3 \cos x+2, a \leq x \leq \frac{\pi}{2}$ where $a<\frac{\pi}{2}$ . By considering the sketched graph of $g(x)$ when $a=-\frac{\pi}{2}$ write down the least value of $a$ such that $g$ has an inverse.
Total Mark	3
Correct Answer	0
Explanation	na
Mark Scheme	The sketch graph looks like the following

Mark Scheme

As the inverse function can only have one value of $y$ for each value of $x, a=0$ Answer: 0

Topic	3.3 Trig functions and identities
Tag	Trigonometry; Trigonometric functions; Sine; Cosine; Tangent; Triangle; Radians; Degrees; Period; Amplitude; Principal axis; Inverse; Trigonometric identities; Angle; Reciprocal
Source	M18/5/MATHL/HP1/ENG/TZ1/XX/3
Question Text	Let $f(x)=\cot (\pi-x) \cos \left(x-\frac{\pi}{2}\right)$ where $0<x<\frac{\pi}{2}$ . Express $f(x)$ in terms of $\sin x$ and $\cos x$ . (a) $\cos x$ (b) $-\cos x$ (c) $\cos x-\sin x$ (d) $\sin x-\cos x$
Total Mark	4
Correct Answer	b
Explanation	na
Mark Scheme	\ $cot (\pi-x) \cos \left(x-\frac{\pi}{2}\right)=-\cot x \sin x=-\cos x$ Answer: B

3.3 Trig functions and identities

Q1

Q2

Q3

Q4

Q5

Q6

Q7

Q8

Q9

Q10

Q11

Q12

Q13