5.2 Properties of Curves

Q1

Topic	5.2 Properties of Curves
Tag	Differentiation Stationary Points Point of Inflection Concavity Tangent Normal L'Hopital's Rule Trigonometric Functions Functions
Source	N17/5/MATHL/HP1/ENG/TZ0/XX/7
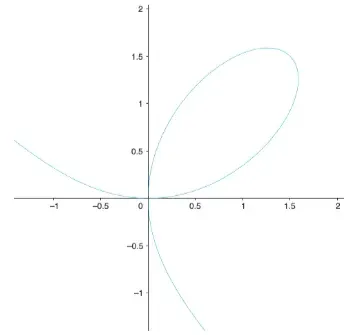
Question Text	The folium of Descartes is a curve defined by the equation $x^3+y^3-3 x y=0$ , shown in the following diagram.

Question Text	The coordinates of the point on the curve where the tangent line is parallel to the $x$ -axis can be written in the form $(\sqrt[3]{a}, \sqrt[3]{b})$ where $a, b \in Z^{+}$ . Find the value of $a$ .
Total Mark	6
Correct Answer	2
Explanation	n/a
Mark Scheme	Tip 2: Parallel to the $x$ -axis means a slope of $0$ . Taking the derivative, $3 x^2+3 y^2 \frac{d y}{d x}-3 x \frac{d y}{d x}-3 y=0$ $\frac{d y}{d x}=\frac{3 y-3 x^2}{3 y^2-3 x} \\ 3 y-3 x^2=0, y=x^2$ Tip 2: Find a way to use the information found In this case $y=x^2$ can be applied to $x^3+y^3-3 x y=0$ So, $x^3+x^6-3 x^3=x^3\left(x^3-2\right)=0$ The coordinates can be written as $(\sqrt[3]{a}, \sqrt[3]{b})$ where $a, b \in Z^{+}$ , so $x=\sqrt[3]{2}$

Q2

Topic	5.2 Properties of Curves
Tag	Differentiation, Trigonometric functions, Quotient Rule
Source	N17/5/MATHL/HP1/ENG/TZ0/XX/11
Question Text	The function $f_n(x)=(\cos 2 x)(\cos 4 x) \ldots\left(\cos 2^n x\right), n \in Z^{+}$ can be written as $f_n(x)=\frac{\sin 2^{n+1} x}{2^n \sin 2 x}, x \neq \frac{m \pi}{2}$ where $m \in Z$ (a)Find an expression for the derivative of $f_n(x)$ with respect to $x$ . (a) $f_n^{\prime}(x)=\frac{\left(2^n \sin 2 x\right)\left(2^{n+1} \cos 2^{n+1} x\right)-\left(\sin 2^{n+1} x\right)\left(2^{n+1} \cos 2 x\right)}{\left(2^n \sin 2 x\right)^2}$ (b) $f_n^{\prime}(x)=\frac{\left(2^n \sin 2 x\right)\left(\cos 2^{n+1} x\right)+\left(\sin 2^{n+1} x\right)\left(2^{n+1} \cos 2 x\right)}{\left(2^2 \sin 2 x\right)^2}$ (c) $f_n^{\prime}(x)=\frac{\left(2^n \sin 2 x\right)\left(2^{n+1} \sin 2^{n+1} x\right)-\left(\cos 2^{n+1} x\right)\left(2^{n+1} \cos 2 x\right)}{\left(2^2 \sin 2 x\right)^2}$ (d) $f_n^{\prime}(x)=\frac{\left(2^n \sin 2 x\right)\left(2^{n+1} \cos 2^n x\right)-\left(\sin 2^{n+1} x\right)\left(2^{n+1} \cos 2 x\right)}{\left(2^n \sin 2 x\right)^2}$
Total Mark	3
Correct Answer	(a)
Explanation	n/a
Mark Scheme	Utilize the quotient rule, $f_n^{\prime}(x)=\frac{\left(2^n \sin 2 x\right)\left(2^{n+1} \cos 2^{n+1} x\right)-\left(\sin 2^{n+1} x\right)\left(2^{n+1} \cos 2 x\right)}{\left(2^n \sin 2 x\right)^2}$
Question Text	(b) For $n>1$ , the equation of the tangent to the curve $y=f_n(x)$ at $x=\frac{\pi}{4}$ is $ax -2 y-\pi=0$ , where $a \in \mathbb{Z}^{+}$ Find the value of $a$
Total Mark	4
Correct Answer	4
Explanation	n/a
Mark Scheme	The slope of the equation $a x-2 y-\pi=0$ is $\frac{a}{2}$ , $f_n^{\prime}\left(\frac{\pi}{4}\right)=\frac{\left(2^n \sin \frac{\pi}{2}\right)\left(2^{n+1} \cos 2^{n+1} \frac{\pi}{4}\right)-\left(\sin 2^{n+1} \frac{\pi}{4}\right)\left(2^{n+1} \cos \frac{\pi}{2}\right)}{\left(2^n \sin \frac{\pi}{2}\right)^2}$ $f_n^{\prime}\left(\frac{\pi}{4}\right)=\frac{\left(2^n\right)\left(2^{n+1} \cos 2^{n+1} \frac{\pi}{4}\right)}{\left(2^n\right)^2} \\$ $f_n^{\prime}\left(\frac{\pi}{4}\right)=2 \cos 2^{n+1} \frac{\pi}{2}$ As $\cos 2^{n+1} \frac{\pi}{2}=\cos 2^{n-1} 2 \pi$ , for $n>1$ $f_n^{\prime}\left(\frac{\pi}{4}\right)=2$ So, $2=\frac{a}{2}$ $a=4$

Q3

Topic	5.2 Properties of Curves
Tag	Differentiation Stationary Points Point of Inflection Concavity Tangent Normal L'Hopital's Rule Trigonometric Functions Functions Graphs Intercepts
Source	M17/5/MATHL/HP1/ENG/TZ1/XX/12 e
Question Text	Consider the function $q(x)=x^5-10 x^2+10 x-1, x \in R$ . (i) The graph of $y=q(x)$ is concave up for $x>a$ where $a$ is a positive integer. Compute the value of $a$ Total Mark: 3 Correct Answer: 1 Explanation: n/a Mark Scheme: $\frac{d^2 y}{d x^2} =20 x^3-20 \\ \text {When } x >1,20 x^3-20>0$ (ii) Find the $x$ -coordinate of the $x$ -intercept of the equation $y = q(x)$ Total Mark: 3 Correct Answer: 1 Explanation: n/a Mark Scheme: by comparing coefficients, $x$ -intercept at $(1,0)$

Q4

Topic	5.2 Properties of Curves
Tag	Differentiation Implicit differentiation Exponential and Logarithmic functions Differentiation Tangent Intercepts Exponential and Logarithmic functions
Source	N16-TZ0-P1-9(HL)
Question Text	A curve has equation $3 x-y^2 e^{2 x}=2$ . (a) Which is the correct expression for $\frac{d y}{d x}$ ? (a) $\frac{d y}{d x}=\frac{3+2 y^3 e^{2 x}}{2 y^2}$ (b) $\frac{d y}{d x}=\frac{3 x-2 y^3 e^{2 x}}{2 y}$ (c) $\frac{d y}{d x}=\frac{3-2 y^2 e^{2 x}}{2 y}$ (d) $\frac{d y}{d x}=\frac{3-y^3 e^{2 x}}{2 y^2}$
Total Mark	4
Correct Answer	(c)
Explanation	n/a
Mark Scheme	Implicit differentiation, $3-\left(2 y \frac{d y}{d x}+2 y^2\right) e^{2 x}=0 \\ \frac{d y}{d x}=\frac{3-2 y^2 e^{2 x}}{2 y}$
Question Text	(b) Select the correct slopes of the equations of tangents to this curve at the points where the curve intersects the line $x = 1$ . (select all that apply) (a) $\frac12$ (b) $\frac{-1}2$ (c) $\frac e2$ (d) $\frac{-e}2$ (e) $e$
Total Mark	4
Correct Answer	(c), (d)
Explanation	n/a
Mark Scheme	$3-y^2 e^2=2 \\ y^2 e^2=1 \\ y= \pm \frac{1}{e}$ $\frac{3-2\left(\frac{1}{e}\right)^2 e^2}{2\left(\frac{1}{e}\right)}=\frac{e}{2} \\ \frac{3-2\left(-\frac{1}{\varepsilon}\right)^2 e^2}{2\left(-\frac{1}{\varepsilon}\right)}=-\frac{e}{2}$

Q5

Topic	5.2 Properties of Curves
Tag	Differentiation, Tangent
Source	M16-TZ1-P1-10(HL)
Question Text	Select the $x$ -coordinates of all the points on the curve $y=x^4+\frac{4}{3} x^3-\frac{13}{2} x^2+7 x+\frac{1}{6}$ at which the tangent to it is parallel to the tangent at the coordinates $(1,3)$ . (select all that apply) (a) -2.5 (b) -1 (c) 0.5 (d) 1 (e) 1.5
Total Mark	7
Correct Answer	(a), (c)
Explanation	n/a
Mark Scheme	$\frac{d y}{d x}=4 x^3+4 x^2-13 x+7$ when $x=1, \frac{d y}{d x}=2$ $4(1)^3+4(1)^2-13(1)+7=2 \\ 4 x^3+4 x^2-13 x+5=0$ Since $x=1$ is a solution to this equation, $(x-1)$ is one factor $(x-1)(2 x-1)(2 x+5)=0$ Thus, $x=0.5, x=-2.5$

Q6

Topic	5.2 Properties of Curves
Tag
Source	N15-TZ0-P1-4(HL)
Question Text	Consider the curve $y=\frac{1}{2-x}, x \in R, x \neq 2$ . (a) Find $\frac{d y}{d x}$ . (a) $\frac{d y}{d x}=\ln (2-x)$ (b) $\frac{d y}{d x}=-\ln (2-x)$ (c) $\frac{d y}{d x}=\frac{1}{(2-x)^2}$ (d) $\frac{d y}{d x}=-\frac{1}{(2-x)^2}$
Total Mark	2
Correct Answer	(c)
Explanation	n/a
Mark Scheme	$\frac{d y}{d x}=(-1)(-1)(2-x)^{-2}=\frac{1}{(2-x)^2}$
Question Text	(b) The equation of the normal to the curve at the point $x = 1$ can be written in the form $ax + by + c = 0$ where $a,b,c ∈ Z$ . Find the value of $a + b + c$ .
Total Mark	4
Correct Answer	0
Explanation	n/a
Mark Scheme	Slope of tangent at $x=1$ $\frac{1}{(2-1)^2}=1$ Slope of normal is $- 1$ As the normal passes through the coordinates $(1,1)$ $y-1=-(x-1) \\ y+x-2$

Q7

Topic	5.2 Properties of Curves
Tag	Differentiation, Tangent, Implicit differentiation Differentiation, Tangent, Implicit differentiation
Source	N15-TZ0-P1-7(HL)
Question Text	A curve is defined by $x y=y^2+9$ . (a) Find the number of horizontal tangents to the curve. (a) 0 (b) 1 (c) 2 (d) 4
Total Mark	4
Correct Answer	(a)
Explanation	n/a
Mark Scheme	Implicit differentiation, $x \frac{d y}{d x}+y=2 y \frac{d y}{d x} \\ \frac{d y}{d x}=\frac{y}{2 y-x}$ Horizontal tangent occurs when $\frac{d y}{d x}=0$ so $y=0$ Thus, $x(0)=(0)^2+9$ However, as $0=9$ is not possible there are no horizontal tangents
Question Text	(b) Select the coordinates of the points where the tangent to the curve is vertical. (select all that apply) (a) $(3,6)$ (b) $(-3, -6)$ (c) $(6, 3)$ (d) $(1, 9)$ (e) $(-1, -9)$
Total Mark	4
Correct Answer	(a), (b)
Explanation	n/a
Mark Scheme	The tangent is vertical when $2 y=x$ $\frac{d y}{d x}=\frac{y}{2 y-x}$ Substitute into the equation, $2 y^2 =y^2+9 \\ y = \pm 3$ Coordinates are, $(3,6)(-3,-6)$

Q8

Topic	5.2 Properties of Curves
Tag	Differentiation Stationary Points Point of Inflection Concavity Tangent Normal L'Hopital's Rule Trigonometric Functions Functions Graphs Intercepts
Source	M15-TZ2-P1-4(HL)
Question Text	Consider the function defined by $f(x)=x^3-6 x^2+20$ . (a) The values of $x$ for which $f(x)$ is a decreasing function can be written as $a<x<b$ where $a, b \in Z$ . Find the value of $a+b$
Total Mark	4
Correct Answer	4
Explanation	n/a
Mark Scheme	Differentiate $f(x)=x^3-6 x^2+4$ $f^{\prime}(x)=3 x^2-12 x=3 x(x-4) \\ x=0, x=4$ So $f$ decreasing on $0<x<4$
Question Text	(b) There is a point of inflexion, $P$ , on the curve $y = f(x)$ . The coordinates of $P$ can be written as $(c, d)$ . Find the value of $c + d$ .
Total Mark	3
Correct Answer	6
Explanation	n/a
Mark Scheme	$f^{\prime \prime}(x)=6 x-12$ To find the point of inflexion set $f^{\prime \prime}(x)=0$ $6 x-12=0 \\ x=2$ Coordinate of $P$ is $(2,4)$

Q9

Topic	5.2 Properties of Curves
Tag	Differentiation Stationary Points Point of Inflection Concavity Tangent Normal L'Hopital's Rule Trigonometric Functions Logarithmic Functions Graphs Intercepts
Source	N14/5/MATHL/HP1/ENG/TZ0/XX/11c
Question Text	The function $g$ is defined as $g(x)=\ln (x-1), x \in R^{+}$ . The graph of $y=g(x)$ intersects the $x$ -axis at the point $Q$ . The equation of the tangent $T$ to the graph of $y=g(x)$ at the point $Q$ can be written as. $y-a x+b=0$ , where $a, b \in Z^{+}$ . Find the value of $a+b$
Total Mark	4
Correct Answer	3
Explanation	n/a
Mark Scheme	$\ln (x-1)=0 \\ x=2$ $x$ -intercept at $(2,0)$ $\frac{d y}{d x}=\frac{1}{x-1}=\frac{1}{2-1}=1 \\ y=x-2 \\ y-x+2=0$

Q10

Topic	5.2 Properties of Curves
Tag	Differentiation Stationary Points Point of Inflection Concavity Tangent Normal L'Hopital's Rule Trigonometric Functions Logarithmic Functions Graphs Intercepts Implicit Differentiation
Source	M14/5/MATHL/HP1/ENG/TZ1/X/9
Question Text	A curve has equation $\operatorname{arctany}^2-\arctan x^2=\frac{\pi}{4}$ . The gradient of the curve at the point where $x=\frac{1}{\sqrt{3}}$ and $y<0$ can be written as $\frac{3 \sqrt{a}}{4}$ where $a$ is a positive integer. Find the value of $a$ .
Total Mark	8
Correct Answer	6
Explanation	N/A
Mark Scheme	$\begin{gathered} \frac{2 y}{1+y^4} \frac{d y}{d x}-\frac{2 x}{1+x^4}=0 \\ \frac{d y}{d x}=\frac{x\left(1+y^4\right)}{y\left(1+x^4\right)} \end{gathered}$ In order to find the coordinate at $x=\frac{1}{\sqrt{3}}$ $\begin{aligned} & \operatorname{arctany}^2-\arctan \left(\frac{1}{3}\right)=\frac{\pi}{4} \\ & \operatorname{arctany}^2=\frac{\pi}{4}+\arctan \left(\frac{1}{3}\right) \\ & y^2=\tan \left(\frac{\pi}{4}+\arctan \left(\frac{1}{3}\right)\right) \\ & =\frac{\tan \frac{\pi}{4}+\tan \left(\arctan \frac{1}{3}\right)}{1-\left(\tan \frac{\pi}{4}\right)\left(\tan \left(\arctan \frac{1}{3}\right)\right)} \\ & =\frac{1+\frac{1}{3}}{1-1 \times \frac{1}{3}}=2 \end{aligned}$ So, $y=\sqrt{2}$ Substitution into $\frac{d y}{d x}$ $\frac{d y}{d x}=\frac{\frac{1}{\sqrt{3}}\left(1+\sqrt{2}^4\right)}{\sqrt{2}\left(1+\left(\frac{1}{\sqrt{3}}\right)^4\right)}=\frac{\frac{5}{\sqrt{3}}}{\frac{10 \sqrt{2}}{9}}=\frac{3 \sqrt{6}}{4}$

Q11

Topic	5.2 Properties of Curves
Tag	Differentiation, Stationary points, Exponential and Logarithmic functions, Quotient rule
Source	M14/5/MATHL/HP1/ENG/TZ1/X/11
Question Text	Consider the function $f(x)=\frac{\ln (x-1)}{x-1}, x>0$ . (a) By finding $f^{\prime}(x)$ , determine the coordinates at which the curve reaches its maximum value. (a) $\left(e+1, \frac{1}{e}\right)$ (b) $\left(e^2+1, \frac{1}{e^2}\right)$ (c) $(2,0)$ (d) $\left(3, \frac{\ln 2}{2}\right)$
Total Mark	3
Correct Answer	(a)
Explanation	n/a
Mark Scheme	$f^{\prime}(x)=\frac{(x-1) \times \frac{1}{x-1}-\ln (x-1)}{(x-1)^2} \\ f^{\prime}(x)=\frac{1-\ln (x-1)}{(x-1)^2}$ Consider $f^{\prime}(x)=0$ $1-\ln (x-1)=0 \\ \ln (x-1)=1 \\ x=e+1 \\ y=\frac{1}{e}$ Hence maximum at the point $\left(e+1, \frac{1}{e}\right)$
Question Text	(b) The equation of the tangent at the $x$ -intercept of the graph of $y = f(x)$ can be written as $2y - ax + b = 0$ where $a, b$ are positive integers.
Total Mark	3
Correct Answer	6
Explanation	n/a
Mark Scheme	$\operatorname{ln}(x - 1) = 0\\ x = 2$ $x$ -intercept $(2, 0)$ $f'(2) = 1 \\y = x - 2 \\2y - 2x + 4 = 0$

Q12

Topic	5.2 Properties of Curves
Tag	Differentiation, Stationary points, Exponential and Logarithmic functions, Quotient rule
Source	N13-TZ0-P1-10(HL)
Question Text	The function $f$ is given by $f(x)=\frac{e^x}{x}$ where $x>0$ . (a) By considering $f^{\prime}(x)$ determine the coordinates of the minimum point. (a) $(1, e)$ (b) $\left(2, e^2\right)$ (c) $(0.5,2 \sqrt{e})$ (d) $\left(0.25,4 e^{\frac{1}{4}}\right)$
Total Mark	3
Correct Answer	(a)
Explanation	n/a
Mark Scheme	$f^{\prime}(x)=\frac{x e^x-e^x}{x^2}$ Set $f^{\prime}(x)=0$ $x e^x-e^x=0 \\$ x=1 Minimum point $(1, e)$
Question Text	(b) The graph of the function $g(x)$ is obtained from the graph $f(x)$ by stretching it horizontally by a scale factor of 3. (i) State the $x$ -coordinate of the minimum for $g(x)$ Total Mark: 2 Correct Answer: 3 Explanation: n/a Mark Scheme: n/a (ii) The $x$ -coordinate of the point where $f(x)=g(x)$ can be written as $\ln\sqrt{a}$ where $a \in Z^{+}$ . Determine the value of $a$ . Total Mark: 2 Correct Answer: 27 Explanation: n/a Mark Scheme: $g(x)=\frac{e^{x / 3}}{x / 3}$ Equating $f(x)=g(x)$ $\frac{e^{x / 3}}{x / 3}=\frac{e^x}{x} \\ 3=e^{\frac{2 x}{3}} \\ \ln 3=\frac{2 x}{3} \\ x=\frac{3}{2} \ln 3=\ln \sqrt{27}$

Q13

Topic	5.2 Properties of Curves
Tag	Intercepts, Exponential and Logarithmic functions
Source	M19/5/MATHL/HP1/ENG/TZ2/XX/11
Question Text	Consider the functions $f$ and $g$ defined by $f(x)=\ln \|x\|, x \in R \backslash\{x \neq 0\}$ and $g(x)=\ln \|x+k\|, x \in R \backslash\{x \neq-k\}$ , where $k \in R, k>2$ . The graphs of $f$ and $g$ intersect at the point $P$ . (a) Find the coordinates of $P$ . (a) $\left(\frac{k}{2}, \ln \frac{k}{2}\right)$ (b) $\left(-\frac{k}{2},-\ln \frac{k}{2}\right)$ (c) $\left(\frac{k}{2},-\ln \frac{k}{2}\right)$ (d) $\left(-\frac{k}{2}, \ln \frac{k}{2}\right)$
Total Mark	2
Correct Answer	(c)
Explanation	n/a
Mark Scheme	At point $P$ , the two functions intersect. $\ln (x+k)=\ln (-x) \\ x=-\frac{k}{2} \\ y=\ln \left(\frac{k}{2}\right)\left(\text { or } y=\ln \left\|\frac{k}{2}\right\|\right)$ Therefore, the coordinates of point $P$ is equal to $\left(-\frac{k}{2}, \ln \frac{k}{2}\right)$ .
Question Text	(b) The tangent to $y = f(x)$ at $P$ passes through the origin $(0,0)$ . The value of $k$ can be expressed as $Ae$ . Find the value of $A$ .
Total Mark	7
Correct Answer	2
Explanation	n/a
Mark Scheme	Attempt to differentiate $\ln (-x)$ or $\ln \|x\|$ , $\frac{d y}{d x}=\frac{1}{x}$ When $x=-\frac{k}{2}, \frac{d y}{d x}=\frac{-2}{k}$ Since the tangent passes through the origin, $\frac{y}{x}=\frac{d y}{d x} \\ \frac{\ln \left(\frac{k}{2}\right)}{-\frac{k}{2}}=\frac{-2}{k} \\ \ln \left(\frac{k}{2}\right)=1 \\ k=2 e$ Hence, the value of $A$ is equal to $2$ .

Q14

Topic	5.2 Properties of Curves
Tag	Differentiation Stationary Points Point of Inflection Concavity Tangent Normal L'Hopital's Rule Trigonometric Functions Logarithmic Functions Graphs Intercepts
Source	M18/5/MATHL/HP1/ENG/TZ1/XX/9
Question Text	Let $f(x)=\frac{4-6 x^5}{4 x^3}, x \in R, x \neq 0$ (a) The graph of $y=f(x)$ has a local maximum at $A$ . The coordinates of $A$ can be expressed as $\left(a, \frac{b}{2}\right)$ . Find the product of $a$ and $b$ .
Total Mark	5
Correct Answer	5
Explanation	n/a
Mark Scheme	Attempt to differentiate $f^{\prime}(x)=-3 x^{-4}-3 x$ At the local maximum, the first derivative value is equal to 0 . $-\frac{3}{x^4}-3 x=0 \\ x^5=-1 \\ x=-1$ Therefore, point $A$ is located at $\left(-1,-\frac{5}{2}\right)$ and $a=-1$ and $b=-5$ . The product of $a$ and $b$ is equal to 5 .
Question Text	(b) There is one point of inflection, $B$ , on the graph of $y=f(x)$ . The coordinates of $B$ can be expressed in the form $B\left(2^a, b \times 2^{-3 a}\right)$ , where $a, b \in Q$ . Find the product of $a$ and $b$ .
Total Mark	8
Correct Answer	-2
Explanation	n/a
Mark Scheme	At the point of inflexion, the second derivative value is equal to $0$ . $f^{\prime \prime}(x)=12 x^{-5}-3=0 \\ x=\sqrt[5]{4}=2^{\frac{2}{5}}$ $a=\frac{2}{5}$ To find the coordinate of $B$ , $f\left(2^{\frac{2}{5}}\right)=\frac{4-6 \times 2^2}{4 \times 2^{\frac{5}{5}}}=-5 \times 2^{-\frac{6}{5}} \\ b=-5$ Hence, the product of $a$ and $b$ is equal to $-2$ .