home
Mission
//////
home
//////

4.1 Statistics

Statistics
Variable
Mean
Median
Mode
Interquartile range
Descriptive
Variance
Standard deviation
Correlation
Data
Cumulative frequency
Line of best fit
Regression
Modeling is a process of creating a mathematical representation of certain real-world scenarios. This falls under the statistics field, which requires some terminology in prior.
Terminology
Definition
Population
Entire collection of individuals about which we want to draw conclusions
Census
Information collected from the whole population
Sample
Subset of population which could be chosen at random to avoid bias
Survey
Collection of information from a sample
Data
Information about individuals in a population
Categorical variable
Describes a particular quality or characteristics which can be divided into different categories
Numerical variable
Describes a characteristic which has a numerical value that can be counted or measured. There are two types: discrete and continuous.
Discrete variable
Takes exact values and is often a result of counting
Continuous variable
Takes numerical values within a certain range, and is often a result of measuring
Random variable
A variable that is subject to random variations so that it can take on multiple different values, each with an associated probability. Often takes XX, YY etc.
Parameter
Numerical quantity that measures some aspect of the population
Statistics
Quantity calculated from data gathered from a sample
Mean
The average of a data set: µ=∑fnµ=\frac{\sum f}{n}
Median
The middle value in a sorted list of numbers. Given nn items,  x~=n+12\tilde{x} = \frac {n+1}2th item
Mode
Most frequently occurring data
Interquartile Range IQR
The difference between the upper quartile (75 percentile) and the lower quartile (25 percentile).
Variance σ2\sigma ^2
The squared deviation from the mean of a random variable.  σ2=∑i=1n(xi−µ)2n\sigma ^2= \frac {\sum _{i=1}^{n}(x_i-µ)^2}{n}
Standard Deviation σ\sigma
Statistical measurement that analyzes the distance of the data from the mean. This is a square root of the variance.  σ=∑i=1n(xi−µ)2n\sigma =\sqrt{\frac{ \sum _{i=1}^{n}(x_i-µ)^2}{n}}
Terminology
Definition
Distribution
The pattern of a variation of data.
Outliers
A value that is much smaller or larger than most of the other values in a set of data. Different tests are utilized to identify the outliers.
Correlation
A measure of a relationship between the two variables
Regression
A method of fitting a curve through a set of points using some goodness-of-fit criterion
There are different ways of organizing the data:
Representation
Features
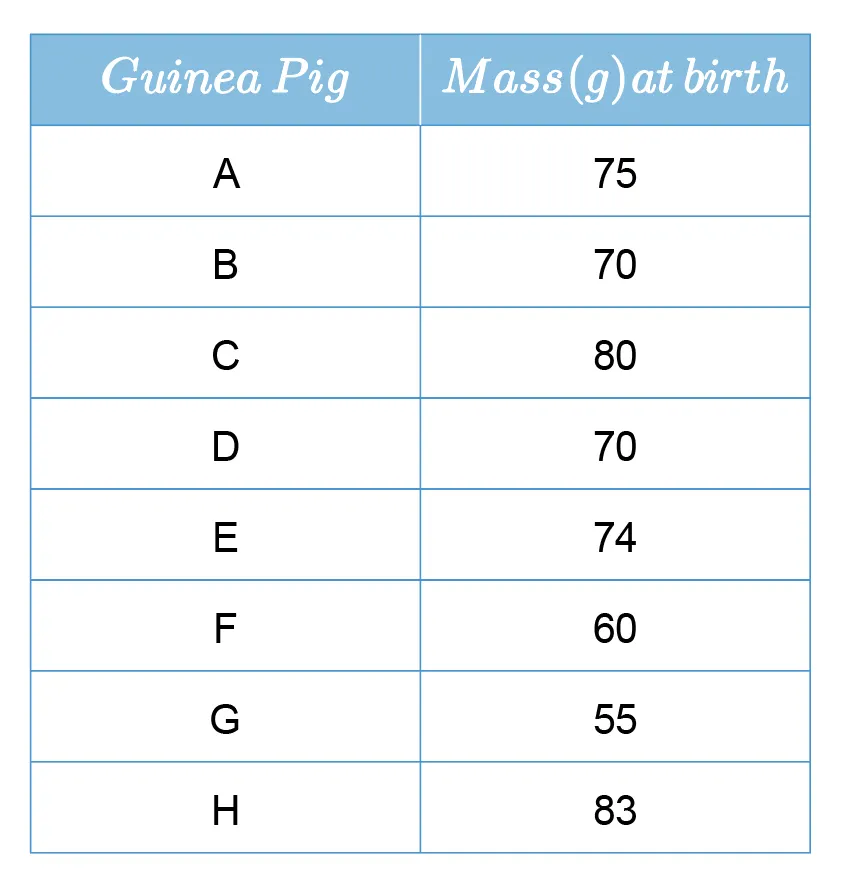
Frequency table
This is a frequency table for categorical variables:
µµ, σ\sigma, σ2\sigma^2 follow the usual formula.
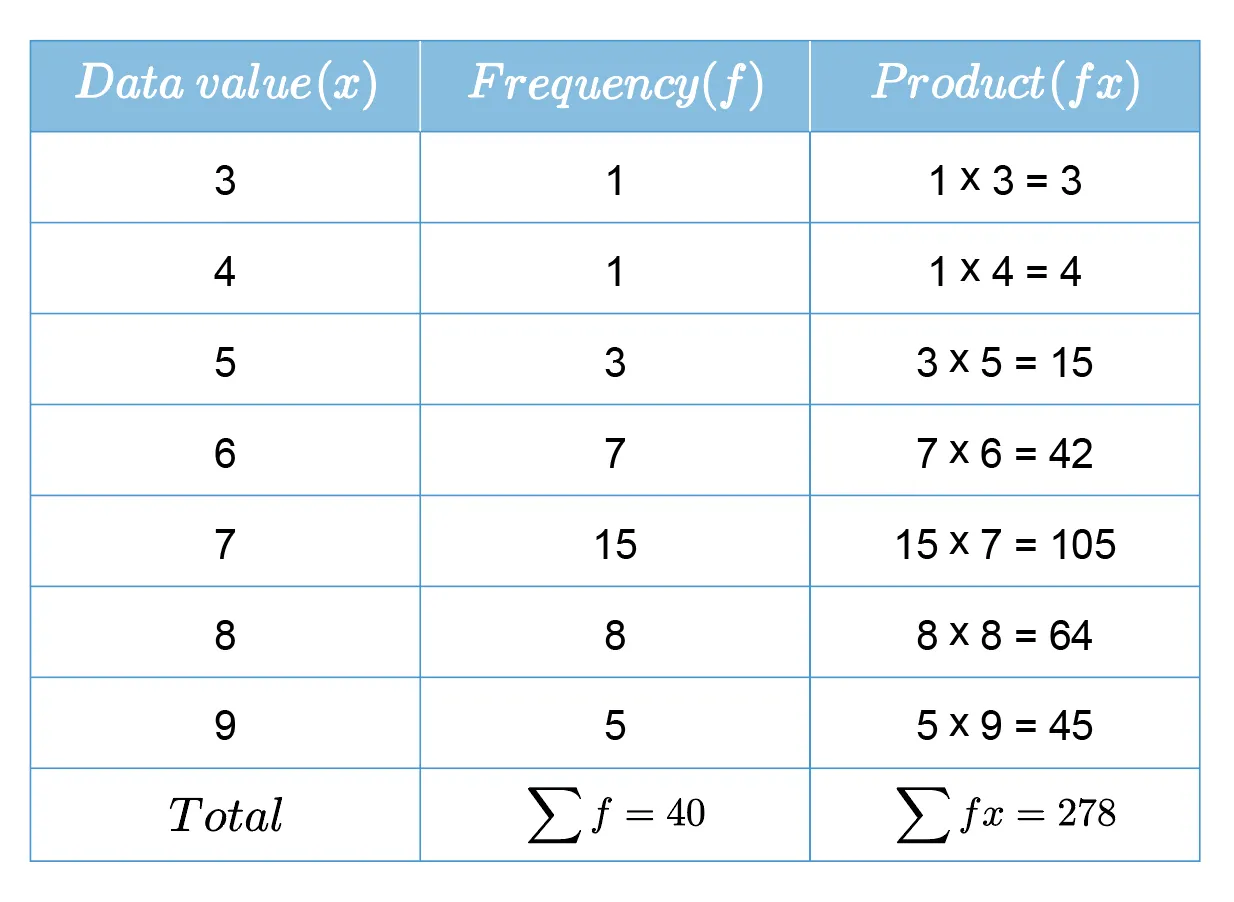
This is a frequency table with numerical variables:
µ=∑fxnµ = \frac{\sum fx}{n}, and other measurements follow the usual formula.
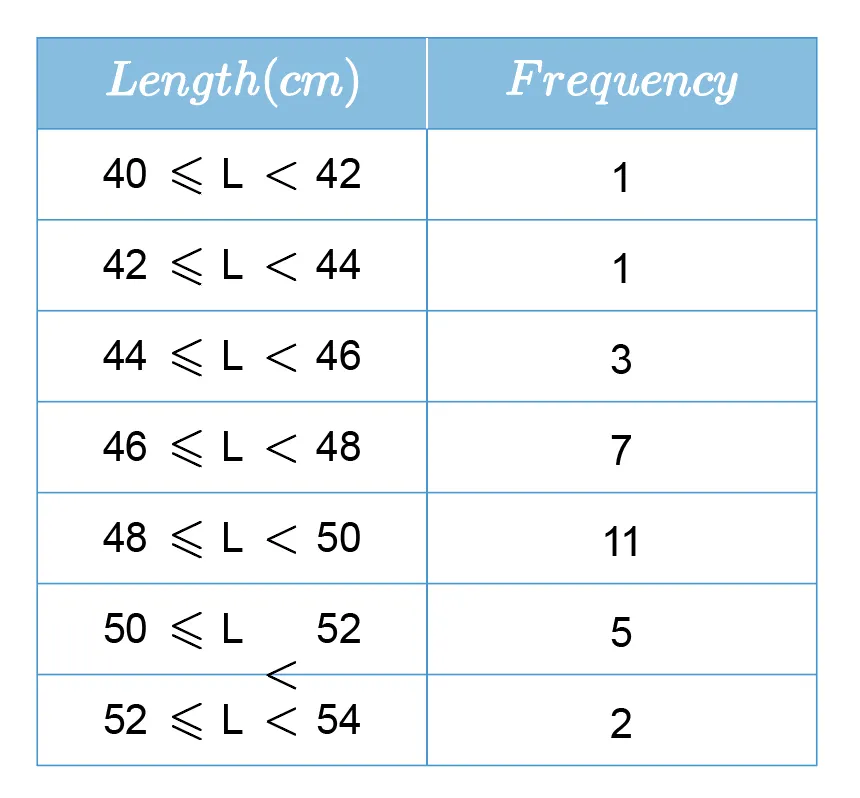
This is a frequency table with class intervals.
µ=∑cavgfnµ =\frac{\sum c_{avg}f}n, and other measurements follow the usual formula.
Histogram
This is a representation of the frequency table in a bar graph.
Box and Whisker plot
If data x>Q3+1.5⋅IQRx > Q3 + 1.5 · IQR or x<Q1−1.5⋅IQRx < Q1 - 1.5 · IQR, this is an outlier.
Cumulative Frequency
Graph of the cumulative frequency with an independent variable.
The derivative of this function is in fact the
probability density function
There are different types of model (regression lines) you can utilize in bivariate statistics.
Model
Features
Line of best fit
Linear regression is used where bivariate statistics follow a linear trend. The line of best fit must pass through the mean point (x‾\overline x, y‾\overline y). The bar notation is used for sample means.
Pearson’s Product-Moment correlation coefficient:
r=∑(x−x‾)(y−y‾)∑(x−x‾)2∑(y−y‾)2 r = \frac {\sum (x-\overline x)(y-\overline y)}{\sqrt {\sum(x-\overline x)^2\sum(y-\overline y)^2}}
rr ranges from −1-1 to 11, and the sign indicates the direction while the size indicates the strength of the correlation.
Coefficient of Determination r2r^2 indicates the degree to which change in the independent variable explains change in the dependent variable.
4.1 Statistics
done
https://docs.google.com/forms/d/e/1FAIpQLSchU5BIrPG2oJbWuFV81y5bXvcs-E5i1sqOcdhlU2xakjTQjw/viewform
4.1 Statistics