A.1 Kinematics

생성일

2024/07/05 08:03

태그

A.1.1 Instantaneous and average

Average Speed : Entire distance covered divided by the amount of time elapsed since it started

•

the average speed is determined solely by a magnitude which excludes the direction

•

the average speed is a scalar quantity so it uses distance, which is also a scalar, to calculate it

•

the equation of average speed is :

\bar{v}= \frac{\Delta x}{\Delta t}

\bar{v}=average\ speed, ∆x=change\ in\ distance, ∆t=change\ in\ time

Instantaneous Velocity

•

Often referred to simply as velocity, is a vector of how quickly an object’s displacement is changing at precisely one specific point somewhere along its route

•

If two points on the path are used to calculate the velocity (separated by a non-zero amount of time), it is instead average velocity

•

the equation of average velocity is :

v = \frac{x(t_{2})-x(t_{2})}{t_{2}-t_{1}}

•

An instantaneous velocity at any time interval is determined by using the following equation :

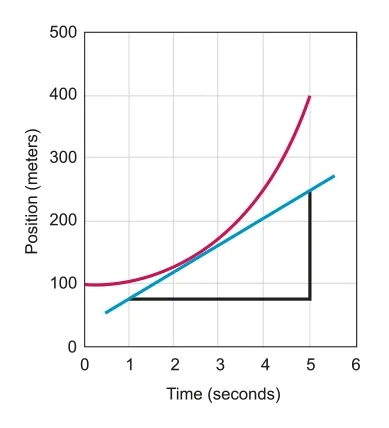
v = \frac{x(t+\Delta t)-x(t)}{\Delta t}=\frac{dx}{dt}\ as\Delta t\to 0

•

Instantaneous velocity can also be interpreted as the slope line tangent to the displacement-time graph at precisely one point.

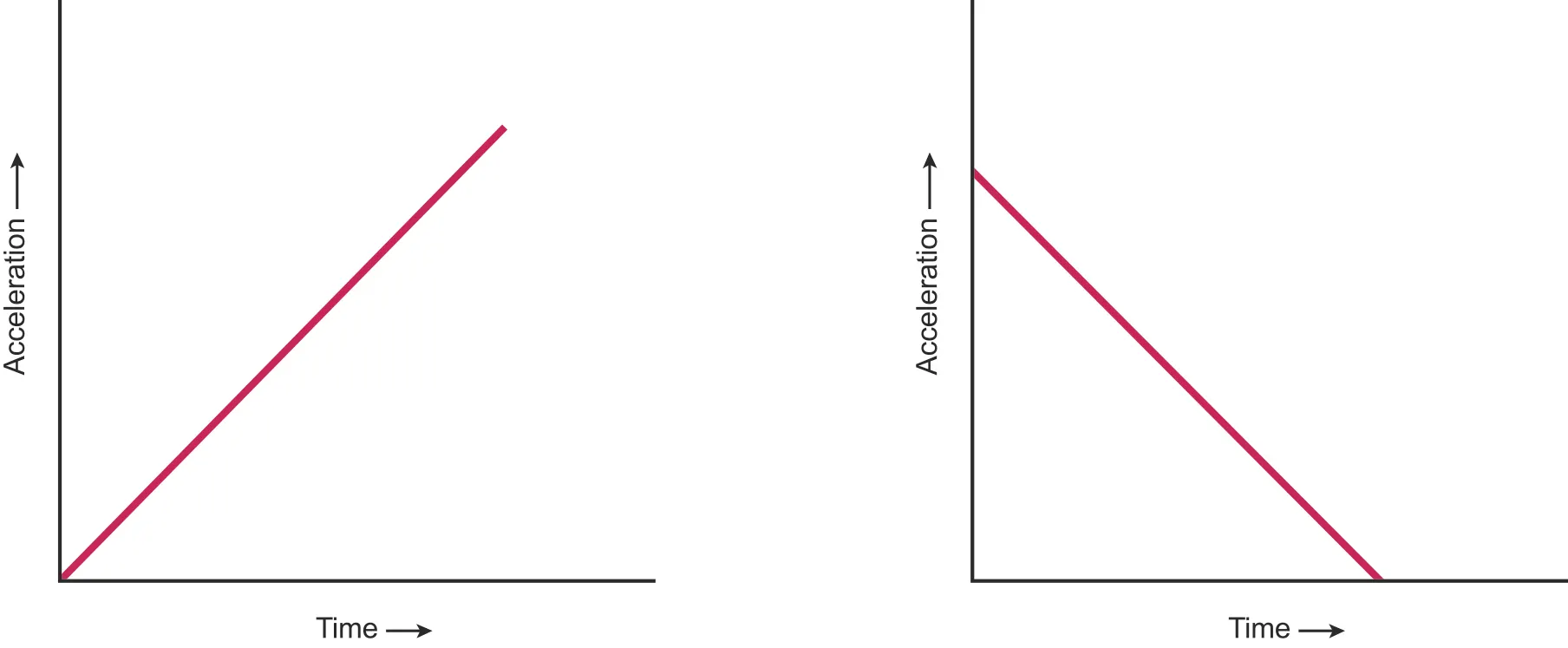
A.1.1-1 Graph representing the acceleration is gradient of velocity

•

Same logic also work for acceleration

A.1.2 Relationship between s, v and a

Definitions of key terminologies

	Symbol	Definition	SI units	Vector or Scalar
Displacement	$s$	Distance moved in a particular direction (final position - initial position)	$m$	Vector
Velocity	$v$	The rate ( $\Delta t$ ) of change of displacement $v=\frac{\Delta s}{\Delta t}$	$m$ /s	Vector
Speed	$v$	The rate of change of distance	$m/s$	Scalar
Acceleration	$a$	The rate of change of velocity	$m/s^{2}$	Vector

Graphical Representation of Motion

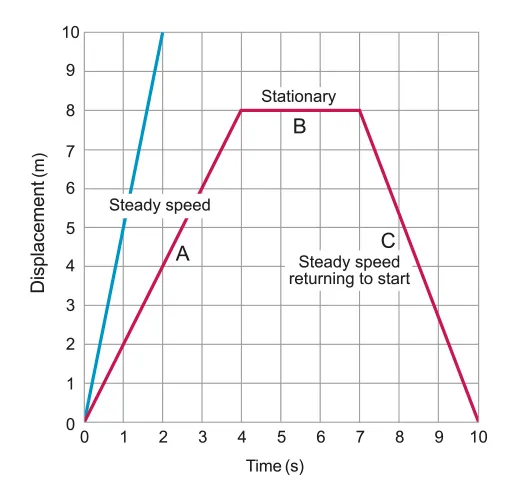
Displacement - Time Graph (s-t graph)

•

The gradient of a s-t graph is velocity

◦

In any graph with a y in the vertical axis and x in the horizontal axis, the gradient is defined as ΔyΔx\frac{\Delta y}{\Delta x}ΔxΔy​. The displacement-time graph has displacement s in the vertical axis and time t in the horizontal axis, so the gradient would be expressed in terms of ss s and t as ΔsΔt\frac{\Delta s}{\Delta t}ΔtΔs​which is the definition of velocity.

◦

The units of the gradient or slope of any graph will always be the units of the vertical axis divided by the units of the horizontal axis. In this case, the vertical axis is displacement measured in units of meters and the horizontal axis is time measured in units of seconds, so the units of the gradient are in m/s which is consistent with the units of velocity.

•

The area under a s-t graph does not represent anything because the units of the area in a graph will be the units of the vertical axis multiplied by the units of the horizontal axis, and meters×seconds\textit{meters} \times \textit{seconds}meters×seconds does not have any meaningful interpretation.

A.1.2-1 Displacement-time Graph representing various motions

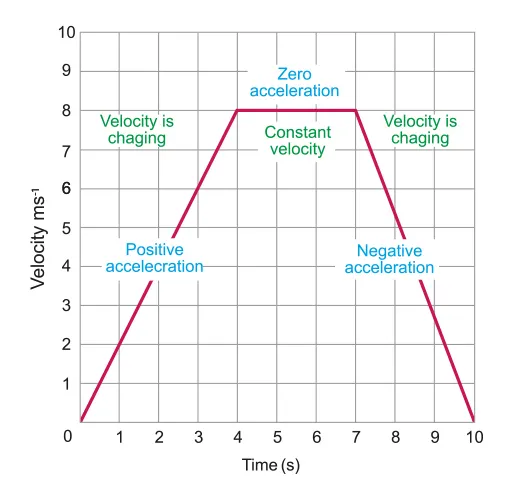
Velocity – Time Graph (v-t graph)

•

The gradient of a v-t graph is acceleration

v\to m/s,a=\frac{\Delta v}{\Delta t}\to \frac{m}{s}\cdot \frac{1}{s}\to m/s^{2}

•

The area under a v-t graph is displacement

v\to m/s, s=v\cdot t\to \frac{m}{s}\cdot s\to m

A.1.2-2 Velocity-time Graph representing various motions

•

In the velocity time graph positive slope refers to that the object is loving in positive direction and its accelerating

•

In velocity time graph straight line refers to that the object is moving in constant velocity

Acceleration – Time Graph (a-t graph)

•

The area of an a-t graph is velocity

A.1.2-3 Acceleration-time graph representing non uniform acceleration and deceleration(in 2023 syllabus)

Exam Techniques (Physics SL/HL)

•

In the IB written examination, many questions deal with the concept of the relationship between s/t, v/t and a/t diagrams

•

If students are familiar with calculus, they may notice that the gradient of a function is found by differentiating the original function

•

The area under the curve is found by integrating the original function

•

Thus, students may roughly generate a function by using the given diagram and taking appropriate action to find a correct solution

Example:

•

A v-t diagram is given :

A.1.2-4 Example of velocity-time graph

•

Find the correct shape of the s-t diagram.

•

Answer should be :

◦

Notice the v-t diagram is having a parabolic shape, thus the equation is roughly dsdt=−t2\frac{ds}{dt}=-t^{2}dtds​=−t2 

\frac{ds}{dt}=-t^{2}

◦

Which is a separable 1st order differential equation, integrate both sides to have

\int ds=\int - t^{2}dt

•

Therefore :

s=-\frac{1}{3}t^{3} + c

A.1.2-5 Velocity-time graph with calculation

A.1.3 SUVAT Equations

SUVAT Equations

•

Suvat equations are five equations that is related to the time, distance, velocity and acceleration especially including projectile motion

•

Calculate displacement (∆s), time (t), initial velocity (u) and final velocity (v) when acceleration is constant

•

The following 4 formulas can be used :

v=u+at \Delta s=\frac{(u+v)}{2}t\Delta s=ut+\frac{1}{2} at^{2}v^{2} =u^{2}+2a\Delta s

A.1.3-1 Projectile motion Example

Algebraic derivation of the SUVAT Equations

•

Acceleration is the rate of change in velocity

•

Under the constant acceleration condition, the v-t diagram has the shape of a linear equation

•

y=mx+cy=mx+c y=mx+c, where m is the slope and c is the y-intercept

•

Since acceleration is the gradient, uuu is the y-interception point of v−tv-t v−t graph

•

The linear equation could be written as v=at+uv=at+uv=at+u

A.1.3-2 Graph with SUVAT explanation

•

∆s could be found in two different approaches

◦

The area of the trapezium :

\Delta s=\frac{upper\ base + bottom\ base}{2}\times height=\frac{(u+v)}{2}t

\Delta s= ut +\frac{1}{2}at^{2}

•

Finally, using two equations v=at+uv=at+uv=at+u and ∆s=ut+12at2∆s=ut+12at2∆s=ut+12at2, we can deduce the derivation of t=v−u/at=v-u/at=v−u/a. Compute into equation ∆s=ut+1/2at2∆s=ut+1/2at2∆s=ut+1/2at2, having that:

\Delta s=u(\frac{v-u}{a})+\frac{1}{2}a(\frac{v-u}{a})^{2} \\ \Delta s=\frac{uv-v^{2}}{a}+\frac{v^{2}+u^{2}-2uv}{2a} \\ 2a\Delta s= v^{2} -u^{2} \\ v^{2} =u^{2}+2as

* HL students may try to derive the above formulas by using calculus.

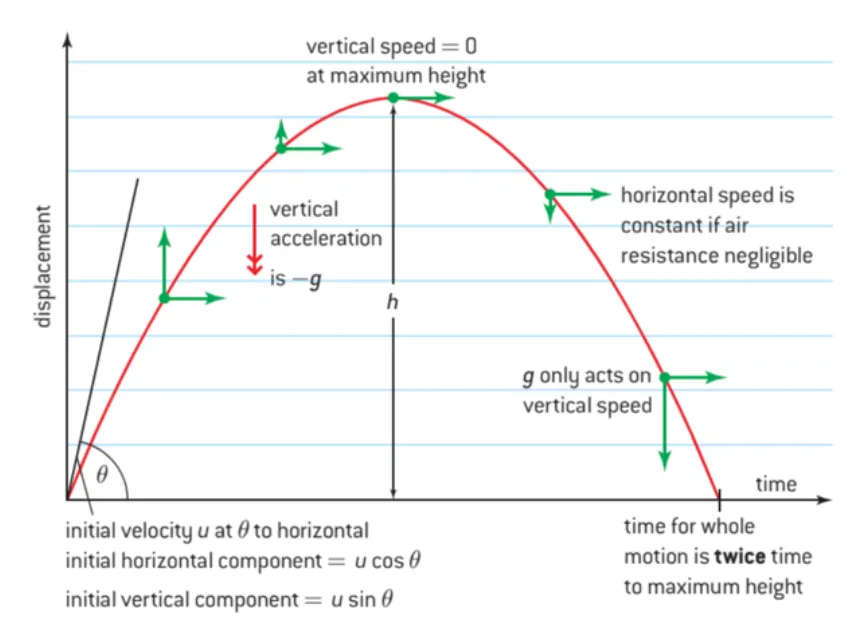
A.1.4 Projectile Motion

Approaching Projectile Motions

•

When an object is doing a projectile motion, we consider its velocity and displacement horizontally and vertically separately

•

It accelerates downwards when an object is released close to the Earth’s surface

•

Now we will derive 4 formulae which can be used to find the following 4 quantities :

◦

Horizontal velocity

◦

Vertical velocity

◦

Horizontal displacement

◦

Vertical displacement

At any time during the projectile motion

•

Given that angle between initial velocity u and horizontal surface is . Since the air resistance is negligible, there is zero resultant force in horizontal direction

•

hence the acceleration in horizontal direction is also 0

•

Thus, the horizontal velocity is always constant which is same as horizontal component of initial velocity

•

Using trig-identity we can find :

v_{x}=ucos\theta

•

Using the formula v=u+atv=u+atv=u+at we derived earlier, substitute velocity and acceleration with velocity and acceleration in vertical direction

•

Meanwhile, set upwards as positive direction, we can find :

v_{y}=usin\theta -gt

•

The horizontal displacement, since air resistance is negligible, ∆s is simply equal time * velocity :

S_{x}=ucos\theta t

Using the general formula

\Delta s= ut + \frac{1}{2}at^{2}

, substitute initial velocity and acceleration with velocity and acceleration in vertical direction, we get the formula of vertical displacement.

S_{y}=usin\theta t -\frac{1}{2}gt^{2}

The maximum height of a projectile motion (vertices) could be found by using the formula

2a\Delta s =v^{2}-u^{2}

As terminal velocity is 0, having that

0=(usin\theta )^{2}-2gh

A.1.4-1 Anotated SUVAT graph

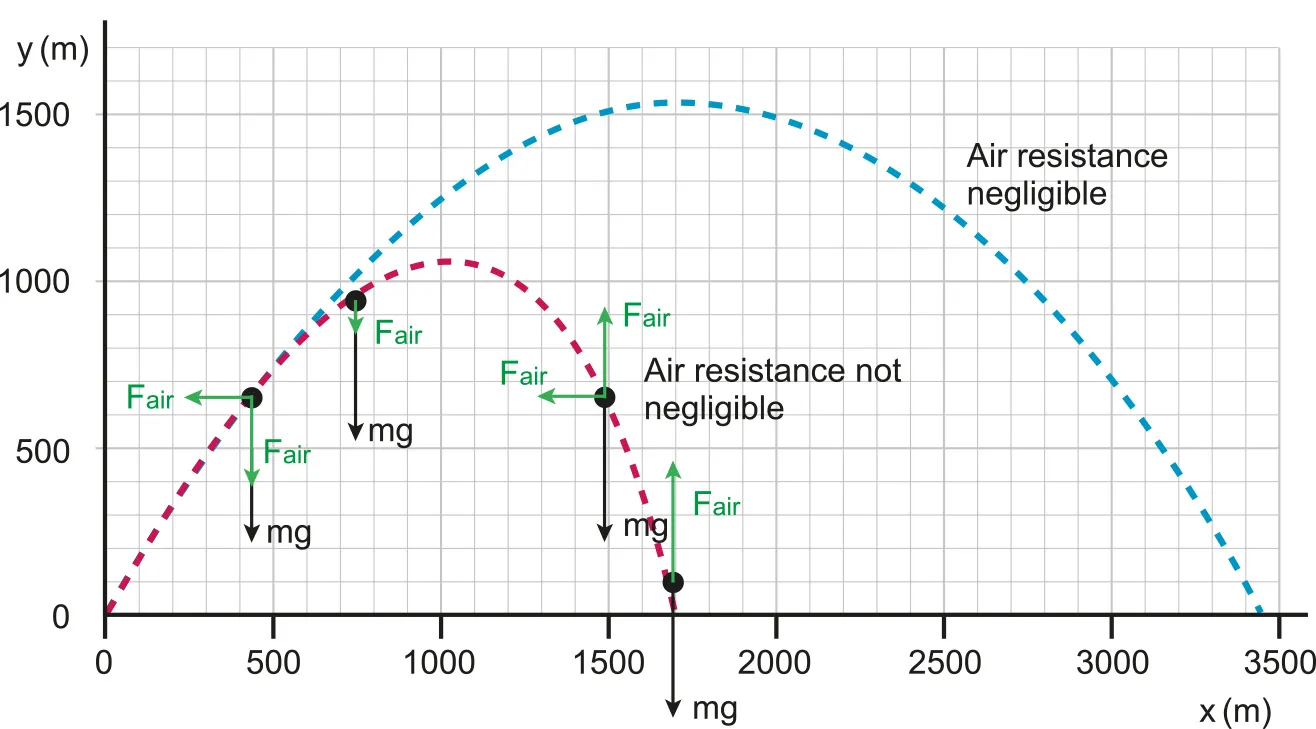
A.1.5 Air resistance and fluid dynamics

Presence of Air Resistance

Low speed	High speed
$F=kv$	$F = kv^{2}$

Air resistance is acting oppositely on the object against the gravitational force

Using Newton 2nd Law:

F = ma

Initial condition 2nd order differential equation could be derived:

mg - k(\frac{dx}{dt})^{2}=m\frac{d^{2}x}{dt^{2}}

x'0=0 and x0=0

x(t)=\frac{mln(cosh(\sqrt{\frac{gk}{m}t})}{k} \\ v(t)=\frac{dx}{dt} =\sqrt{\frac{mg}{k}} tanh(\sqrt{\frac{gk}{m}t})

Taking limits of t→∞, terminal velocity could be derived

max(v(t))=\sqrt{\frac{mg}{k}}

Thus, when there is air resistance, object will reach a constant velocity after a time interval. (when air resistance is equal to the gravitational force)

•

horizontal velocity will eventually approach zero

•

vertical velocity upwards will decrease faster than if only gravity were considered lower max height so a > g

•

a=g only when v=0 at the peak

•

when going down a<g so the magnitude of vertical velocity down increases more slowly than if only gravity were considered

•

at terminal velocity a=0 since Fg=Fd

•

velocity and acceleration graphs needed showing the effect of drag no drag

•

effect of parachute on velocity and acceleration on another v-t graph and a-t graph

A.1.5-1 Notated SUVAT graph with air resistance

With Air resistance	Without Air resistance
Maximum height reached is lower	Maximum height reached is higher
Horizontal displacement is smaller	Horizontal displacement reached is larger