Integration is an inverse operation of differentiation.
Thus, we call as the antiderivative of , and .
Indefinite integral denotes an integration without the bounds, and thus has a constant of integration .
Figure 5.5.1 Definite integral represented as the area under the curve for a specific range
Definite integral denotes an integration with the bounds, and represents the area below from to .
Given as the antiderivative of , . (Fundamental theorem of calculus.)
Integrals have different properties:
1.
2.
3.
4.
5.
We have different techniques to solve the integration.
Method | Steps |
Integration by substitution | Integration by substitution is the reverse process of differentiating using the chain rule.
Suppose is the antiderivative of , so .
(1)
Since {chain rule}
Hence, (2)
Let (1) equal to (2), then it can be concluded that: .
Replace the complicated expression to any parameter of your choice: , etc.
1. If there is a bracket, or root, try substitution for the expression within the bracket or the root. (ex: , )
2. If there is an exponential, try substitution for the exponent. (ex: )
3. If it is a fraction, try substitution for the denominator. (ex: )
4. In any other case, try to see whether the derivative of your target substitution is included in the integrand. If so, that is most likely the correct substitution.
Trigonometric substitution:
1.
2.
3.
Draw a triangle to express different functions of in terms of .
*Remember to change the bound of the integration if you are dealing with a definite integral. |
Integration by parts (HL) | This rises from the product rule of differentiation.
Since
{product rule}
.
This rule allows us to find provided can be found.
Generally, the function that becomes simpler when differentiated should be assigned to . The acronym is LIPET (Logarithmic, inverse trig, polynomial, exponential, and trig functions).
Step 1. Assign and .
Differentiate to find and integrate to find .
For example,
For ,
Step 2. Apply the integration by parts formula.
Step 3. Work out the second integral, .
Other rules of differentiation and integration, such as chain rule and substitution, may be applied together with integration by parts.
Integration of single functions by parts
(For example, , , , and .)
Rewrite the single function as , and let and .
Repeated integration by parts
Integration by parts can be repeated to the second integral if the second integral is a product of two functions of .
Integration by parts may also end up in a loop.
Consider
The derivative of is , and the derivative of is ; have derivative . Hence, the integrated product would involve either or ; the second integral becomes identical to (or a multiple of) the original integral.
In such a case, name the original integral as .
then appears twice in integration by parts.
For example, , where are parts of the integral not requiring further work.
Then, rearrange the equation to isolate the .
|
Partial fractions (HL) | Partial fractions are decomposed parts of a complex rational expression, rewritten as the sum of fractions.
Each partial fraction has a denominator of a linear factor of the denominator of the rational expression.
(1)
Substituting into (1),
Substituting into (1),
Hence, .
(If the rational expression can be written in the form , integration by substitution is suitable, rather than partial fractions.)
First, write the quotient in the integral as the sum of partial fractions by factorizing the denominator.
For example,
Then, integrate each partial fraction, which leads to an expression involving the sum of natural logarithms.
For example, |
We can estimate the area under the curve (i.e. ) numerically.
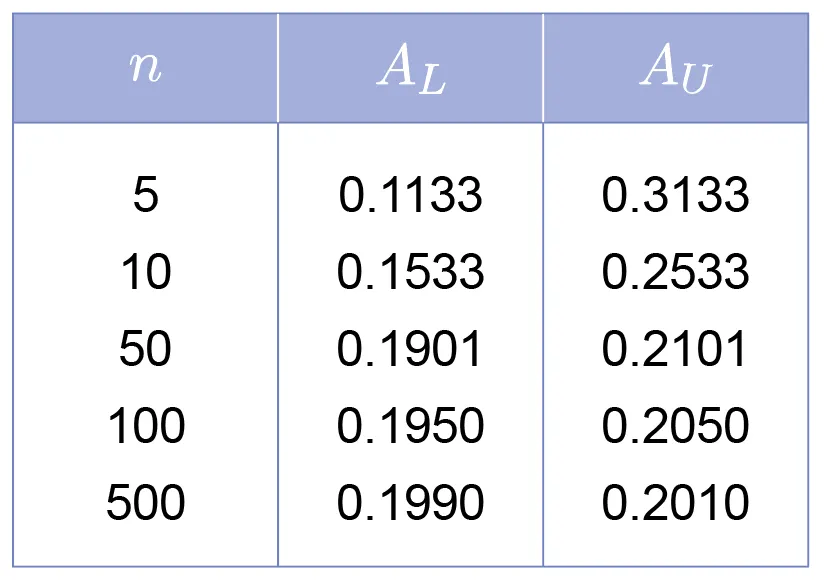
Both use different numbers of partitions, a subdivision of a given interval into non-empty sets.
For instance, if we divide into subintervals, we obtain equal width of per partition. Then, we have , and the th subinterval would be: .
Method
Riemann Sum (HL)
Definition
Riemann Sum utilizes the lower sum and the upper sum .
Since the function is increasing, we have: .
Then, as where , using the squeeze theorem:
yields .
Apply this formula after constructing an appropriate table of subintervals.
*This is the definition of Riemann Integral.
*The more subintervals (i.e. ) we take, the more accurate our approximation becomes.