home
Mission
///////
home
///////

5.4 Integration

Q1

Topic
5.4 Integration
Tag
Source
M17/5/MATHL/HP1/ENG/TZ1/11
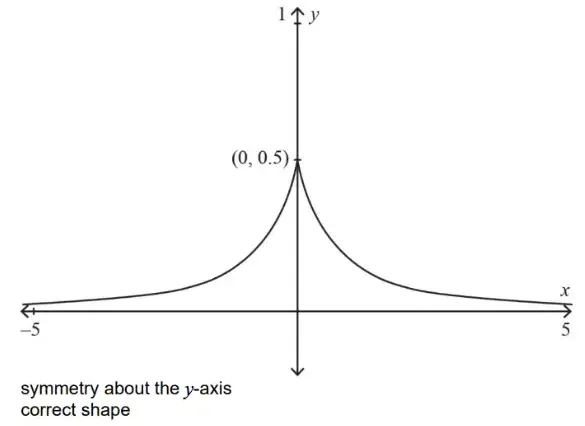
Question Text
Consider the function f(x)=2x2+4x+3,x∈R,x≠−3,x≠−1f(x)=\frac{2}{x^2+4 x+3}, x \in R, x \neq-3, x \neq-1 . (a) Find the value of pp if ∫01f(x)dx=ln⁡(pq)\int_0^1 f(x) d x=\ln \left(\frac{p}{q}\right), where pp and qq are positive integers in lowest terms
Total Mark
4
Correct Answer
3
Explanation
na
Mark Scheme
Tip 1: Notice that the integral can be simplified using partial fractions f(x)=2x2+4x+3=1x+1−1x+3∫011x+1−1x+3dx=[ln⁡(x+1)−ln⁡(x+3)]01=ln⁡2−ln⁡4−ln⁡1+ln⁡3=ln⁡(32)\begin{aligned} & f(x)=\frac{2}{x^2+4 x+3}=\frac{1}{x+1}-\frac{1}{x+3} \\ & \int_0^1 \frac{1}{x+1}-\frac{1}{x+3} d x=[\ln (x+1)-\ln (x+3)]_0^1 \\ & =\ln 2-\ln 4-\ln 1+\ln 3=\ln \left(\frac{3}{2}\right) \end{aligned} Answer: 3
Question Text
(b) The area of the region enclosed between the graph of y=f(∣x∣)y=f(|x|), the xx-axis and the lines with equations x=−1x=-1 and x=1x=1 can be written as ln⁡(ab)\ln \left(\frac{a}{b}\right) where aa and bb are positive integers in lowest terms. Find the value of a+ba+b.
Total Mark
5
Correct Answer
13
Explanation
na
Mark Scheme
Mark Scheme
As the graph is symmetrical across the y-axis, the area is equal to 2∫01f(x)dx=2ln⁡(32)=ln⁡(94)2 \int_0^1 f(x) d x=2 \ln \left(\frac{3}{2}\right)=\ln \left(\frac{9}{4}\right) Answer: 13

Q2

Topic
5.4 Integration
Tag
Integration, Indefinite integral, By parts, Substitution, Trigonometric functions
Source
M17/5/MATHL/HP1/ENG/TZ1/9
Question Text
Select all the terms that appear when finding ∫arcsin⁡xdx\int \arcsin x d x. (a) xarcsin⁡xx \arcsin x (b) arcsin⁡x\arcsin x (c) −1−x2-\sqrt{1-x^2} (d) 1−x2\sqrt{1-x^2} (e) ln⁡∣1−x2∣\ln \left|1-x^2\right|
Total Mark
5
Correct Answer
a,d
Explanation
na
Mark Scheme
Attempt at integration by parts with u=arcsin⁡xu=\arcsin x and v′=1v^{\prime}=1. ∫arcsin⁡xdx=xarcsin⁡x−∫x1−x2dx\int \arcsin x d x=x \arcsin x-\int \frac{x}{\sqrt{1-x^2}} d x Solve ∫x1−x2dx\int \frac{x}{\sqrt{1-x^2}} d x by substitution with u=1−x2u=1-x^2. u=1−x2du=−2xdxdx=−du2x∫x1−x2dx=−12∫1udu=−1−x2+C\begin{gathered} u=1-x^2 \\ d u=-2 x d x \\ d x=-\frac{d u}{2 x} \\ \int \frac{x}{\sqrt{1-x^2}} d x=-\frac{1}{2} \int \frac{1}{\sqrt{u}} d u=-\sqrt{1-x^2}+C \end{gathered} Hence, ∫arcsin⁡xdx=arcsin⁡x+1−x2+C\int \arcsin x d x=\arcsin x+\sqrt{1-x^2}+C Answer: A, D

Q3

Topic
5.4 Integration
Tag
Integration, Definite integral, Substitution, Trigonometric functions
Source
M17/5/MATHL/HP1/ENG/TZ2/6
Question Text
(a) Using the substitution x=tan⁡θx=\tan \theta find ∫011(x2+1)2dx\int_0^1 \frac{1}{\left(x^2+1\right)^2} d x. [multiple choice] (a) ∫01cos⁡2θdθ\int_0^1 \cos ^2 \theta d \theta (b) ∫01sec⁡θdθ\int_0^1 \sec \theta d \theta (c) ∫0π4sec⁡θdθ\int_0^{\frac{\pi}{4}} \sec \theta d \theta (d) ∫0π4cos⁡2θdθ\int_0^{\frac{\pi}{4}} \cos ^2 \theta d \theta
Total Mark
4
Correct Answer
d
Explanation
na
Mark Scheme
Let x=tan⁡θ,dx=sec⁡2θdθx=\tan \theta, d x=\sec ^2 \theta d \theta Before substituting xx, we need to adjust the upper and lower limits.  when x=1,θ=π4 when x=0,θ=0\begin{aligned} & \text { when } x=1, \theta=\frac{\pi}{4} \\ & \text { when } x=0, \theta=0 \end{aligned} Next, we can use the substitution rule. ∫011(x2+1)2dx=∫0π41(tan⁡2θ+1)2⋅sec⁡2θdθ=∫0π4cos⁡2θdθ\int_0^1 \frac{1}{\left(x^2+1\right)^2} d x=\int_0^{\frac{\pi}{4}} \frac{1}{\left(\tan ^2 \theta+1\right)^2} \cdot \sec ^2 \theta d \theta=\int_0^{\frac{\pi}{4}} \cos ^2 \theta d \theta Answer: D
Question Text
(b) Hence find the value of ∫011(x2+1)2dx\int_0^1 \frac{1}{\left(x^2+1\right)^2} d x. [multiple choice] (a) π8+14\frac{\pi}{8}+\frac{1}{4} (b) π8−14\frac{\pi}{8}-\frac{1}{4} (c) π4+12\frac{\pi}{4}+\frac{1}{2} (d) π4−12\frac{\pi}{4}-\frac{1}{2}
Total Mark
3
Correct Answer
a
Explanation
na
Mark Scheme
To find the value of ∫011(x2+1)2dx\int_0^1 \frac{1}{\left(x^2+1\right)^2} d x, we can use the limits of integration. ∫011(x2+1)2dx=∫0π4cos⁡2θdθ=12∫0π4(1+cos⁡2θ)dθ=12[θ+sin⁡2θ2]0π4=π8+14\int_0^1 \frac{1}{\left(x^2+1\right)^2} d x=\int_0^{\frac{\pi}{4}} \cos ^2 \theta d \theta=\frac{1}{2} \int_0^{\frac{\pi}{4}}(1+\cos 2 \theta) d \theta=\frac{1}{2}\left[\theta+\frac{\sin 2 \theta}{2}\right]_0^{\frac{\pi}{4}}=\frac{\pi}{8}+\frac{1}{4} Answer: A

Q4

Topic
5.4 Integration
Tag
Integration, Indefinite integral, By parts, Trigonometric functions
Source
M17/5/MATHL/HP1/ENG/TZ2/XX/9
Question Text
Consider the function ff defined by f(x)=x2−a2,x∈Rf(x)=x^2-a^2, x \in R where aa is a positive constant. (a) Select all the terms that appear in the value of ∫f(x)sin⁡xdx\int f(x) \sin x d x. (a) a2cos⁡xa^2 \cos x (b) −x2cos⁡x-x^2 \cos x (c) 2cos⁡x2 \cos x (d) 2xsin⁡x2 x \sin x (e) 2sin⁡x2 \sin x
Total Mark
5
Correct Answer
a,b,c,d
Explanation
na
Mark Scheme
Attempt at integration by parts ∫(x2−a2)sin⁡xdx=∫x2sin⁡xdx−∫a2sin⁡xdx=−x2cos⁡xdx+∫2xcos⁡xdx−∫a2sin⁡xdx=−x2cos⁡x+2sin⁡x−2∫sin⁡xdx−∫a2sin⁡xdx=−x2cos⁡x+2xsin⁡x+2cos⁡x+a2cos⁡x+C\begin{aligned} & \int\left(x^2-a^2\right) \sin x d x=\int x^2 \sin x d x-\int a^2 \sin x d x \\ = & -x^2 \cos x d x+\int 2 x \cos x d x-\int a^2 \sin x d x \\ = & -x^2 \cos x+2 \sin x-2 \int \sin x d x-\int a^2 \sin x d x \\ = & -x^2 \cos x+2 x \sin x+2 \cos x+a^2 \cos x+C \end{aligned} Answer: A, B, C, D
Question Text
(b) The function gg is defined by g(x)=xf(x)g(x)=x \sqrt{f(x)} for ∣x∣>a|x|>a. By finding g′(x)g^{\prime}(x) determine if gg is an increasing or decreasing function. [multiple choice] (a) Increasing (b) Decreasing
Total Mark
4
Correct Answer
a
Explanation
na
Mark Scheme
Use the product rule. g(x)=x(x2−a2)12g′(x)=(x2−a2)12+12x(x2−a2)12(2x)g′(x)=(x2−a2)12+x2(x2−a2)−12\begin{gathered} g(x)=x\left(x^2-a^2\right)^{\frac{1}{2}} \\ g^{\prime}(x)=\left(x^2-a^2\right)^{\frac{1}{2}}+\frac{1}{2} x\left(x^2-a^2\right)^{\frac{1}{2}}(2 x) \\ g^{\prime}(x)=\left(x^2-a^2\right)^{\frac{1}{2}}+x^2\left(x^2-a^2\right)^{-\frac{1}{2}} \end{gathered} Both parts of the expression are positive. Since g′(x)g^{\prime}(x) is the sum of two positive values, g′(x)g^{\prime}(x) is always positive. Therefore, gg is an increasing function. Answer: A

Q5

Topic
5.4 Integration
Tag
Integration, Definite integral, Trigonometric functions
Source
M16-TZ2-P1-3(HL)
Question Text
Given that cot⁡α=tan⁡(π2−α)\cot \alpha=\tan \left(\frac{\pi}{2}-\alpha\right) for 0<α<π20<\alpha<\frac{\pi}{2}, find ∫tan⁡αcot⁡a11+x2dx,0<α<π2\int_{\tan \alpha}^{\cot a} \frac{1}{1+x^2} d x, 0<\alpha<\frac{\pi}{2}. [4] [multiple choice] (a) −2α-2 \alpha (b) π2+2α\frac{\pi}{2}+2 \alpha (c) π2−2α\frac{\pi}{2}-2 \alpha (d) π2\frac{\pi}{2}
Total Mark
4
Correct Answer
c
Explanation
na
Mark Scheme
∫tan⁡αcot⁡α11+x2dx=[arctan⁡x]tan⁡αcot⁡α∫tan⁡αcot⁡α11+x2dx=arctan⁡(cot⁡α)−arctan⁡(tan⁡α)\begin{gathered} \int_{\tan \alpha}^{\cot \alpha} \frac{1}{1+x^2} d x=[\arctan x]_{\tan \alpha}^{\cot \alpha} \\ \int_{\tan \alpha}^{\cot \alpha} \frac{1}{1+x^2} d x=\arctan (\cot \alpha)-\arctan (\tan \alpha) \end{gathered} Using the given information that cot⁡α=tan⁡(π2−α)\cot \alpha=\tan \left(\frac{\pi}{2}-\alpha\right), ∫tan⁡αcot⁡α11+x2dx=arctan⁡(tan⁡(π2−α))−arctan⁡(tan⁡α)∫tan⁡αcot⁡α11+x2dx=π2−α−α=π2−2α\begin{gathered} \int_{\tan \alpha}^{\cot \alpha} \frac{1}{1+x^2} d x=\arctan \left(\tan \left(\frac{\pi}{2}-\alpha\right)\right)-\arctan (\tan \alpha) \\ \int_{\tan \alpha}^{\cot \alpha} \frac{1}{1+x^2} d x=\frac{\pi}{2}-\alpha-\alpha=\frac{\pi}{2}-2 \alpha \end{gathered} Answer: C

Q6

Topic
5.4 Integration
Tag
Integration, Indefinite integral, By parts, Trigonometric functions
Source
N15-TZ0-P1-2(HL)
Question Text
Select all the terms that appear in the value of ∫xsin⁡xdx\int x \sin x d x. (a) xcos⁡xx \cos x (b) −xcos⁡x-x \cos x (c) sin⁡x\sin x (d) −sin⁡x-\sin x (e) xsin⁡xx \sin x
Total Mark
4
Correct Answer
b,c
Explanation
na
Mark Scheme
Attempt integration by parts. ∫xsin⁡xdx=−xcos⁡x+∫cos⁡xdx=−xcos⁡x+sin⁡x+C\int x \sin x d x=-x \cos x+\int \cos x d x=-x \cos x+\sin x+C Answer: B, C

Q7

Topic
5.4 Integration
Tag
Integration, Definite integral, Substitution, Exponential and Logarithmic functions
Source
N15-TZ0-P1-5(HL)
Question Text
Given that u=ln⁡xu=\ln x, use integration by substitution to find the value of ∫ee2dxxln⁡x\int_e^{e^2} \frac{d x}{x \ln x}. (a) 0 (b) −12-\frac{1}{2} (c) 12\frac{1}{2} (d) ln⁡2\ln 2
Total Mark
4
Correct Answer
d
Explanation
n/a
Mark Scheme
When u=ln⁡x,dudx=1xdxu=\ln x, \frac{d u}{d x}=\frac{1}{x} d x Before substituting xx, we need to adjust the upper and lower limits. when x=e2,u=2x=e^2, u=2 when x=e,θ=1x=e, \theta=1 Next, we integrate using substitution. ∫ee2dxxln⁡x=∫121udu=[ln⁡u]12=ln⁡2−ln⁡1=ln⁡2\int_e^{e^2} \frac{d x}{x \ln x}=\int_1^2 \frac{1}{u} d u=[\ln u]_1^2=\ln 2-\ln 1=\ln 2 Answer: D

Q8

Topic
5.4 Integration
Tag
Integration Indefinite Integral Definite Integral Substitution By Parts Partial Fractions Riemann Sum Trigonometric Functions Logarithmic Functions Area
Source
N15-TZ0-P1-12(HL)
Question Text
Consider the function defined by f(x)=2x1−2x2f(x)=2 x \sqrt{1-2 x^2} on the domain −1≤x≤1-1 \leq x \leq 1. (a) Determine if ff is an even or odd function. [multiple choice] (a) Even (b) Odd
Total Mark
2
Correct Answer
b
Explanation
n/a
Mark Scheme
−f(x)=−2x1−2x2f(−x)=2(−x)1−2x2=−2x1−2x2\begin{gathered} -f(x)=-2 x \sqrt{1-2 x^2} \\ f(-x)=2(-x) \sqrt{1-2 x^2}=-2 x \sqrt{1-2 x^2} \end{gathered} Since −f(x)=f(−x),f-f(x)=f(-x), f is an odd function. Answer: B
Question Text
(b) Hence find the xx-coordinates of any local maximum or minimum points. [multiple choice] (a) 12\frac{1}{\sqrt{2}} (b) −12-\frac{1}{\sqrt{2}} (c) 12\frac{1}{2} (d) −12-\frac{1}{2} (e) 0
Total Mark
3
Correct Answer
c,d
Explanation
na
Mark Scheme
First, we must find the first derivative of ff. f′(x)=2x⋅12(1−2x2)−12⋅(−4x)+2(1−2x2)12f′(x)=21−x2−4x21−2x2=2−8x21−2x2\begin{gathered} f^{\prime}(x)=2 x \cdot \frac{1}{2}\left(1-2 x^2\right)^{-\frac{1}{2}} \cdot(-4 x)+2\left(1-2 x^2\right)^{\frac{1}{2}} \\ f^{\prime}(x)=2 \sqrt{1-x^2}-\frac{4 x^2}{\sqrt{1-2 x^2}}=\frac{2-8 x^2}{\sqrt{1-2 x^2}} \end{gathered} On the local maximum and minimum, the first derivative value is equal to 0 . f′(x)=02−8x2=0x=±12\begin{gathered} f^{\prime}(x)=0 \\ 2-8 x^2=0 \\ x= \pm \frac{1}{2} \end{gathered} Hence, the xx-coordinate of the local maximum and minimum is 12\frac{1}{2} and −12-\frac{1}{2}. Answer: C, D
Question Text
(c) Find the range of ff. [multiple choice] (a) [−22,1]\left[-\frac{\sqrt{2}}{2}, 1\right] (b) [−1,22]\left[-1, \frac{\sqrt{2}}{2}\right] (c) [−22,22]\left[-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right] (d) [−1,1][-1,1]
Total Mark
3
Correct Answer
c
Explanation
na
Mark Scheme
Find the y-coordinates of the local maximum and minimum points. f(12)=22,f(−12)=−22f\left(\frac{1}{2}\right)=\frac{\sqrt{2}}{2}, f\left(-\frac{1}{2}\right)=-\frac{\sqrt{2}}{2} Hence, the range of f(x)f(x) is [−22,22]\left[-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right] Answer: C
Question Text
(d) Find all xx intercepts of ff. [multiple choice] (a) 12\frac{1}{\sqrt{2}} (b) −12-\frac{1}{\sqrt{2}} (c) 12\frac{1}{2} (d) −12-\frac{1}{2} (e) 0
Total Mark
2
Correct Answer
a,b,e
Explanation
na
Mark Scheme
To find the x -intercept, we must find f(x)=0f(x)=0. 2x1−2x2=0x=0 or x=±22\begin{gathered} 2 x \sqrt{1-2 x^2}=0 \\ x=0 \text { or } x= \pm \frac{\sqrt{2}}{2} \end{gathered} Answer: A, B, E
Question Text
(e) The area of the region enclosed by the graph y=f(x)y=f(x) and the xx-axis for x≥0x \geq 0 can be expressed as 1a\frac{1}{a}. Find the value of aa.
Total Mark
4
Correct Answer
3
Explanation
na
Mark Scheme
We can find the area enclosed by f(x)f(x) and the xx-axis using the limits of integration. A=∫0222x1−2x2dxA=\int_0^{\frac{\sqrt{2}}{2}} 2 x \sqrt{1-2 x^2} d x Attempt at backwards chain rule or substitution. −12∫022(−4x)1−2x2dx=−12⋅[23(1−2x2)32]022=−13⋅[(1−2x2)32]022=0−(−13)=13-\frac{1}{2} \int_0^{\frac{\sqrt{2}}{2}}(-4 x) \sqrt{1-2 x^2} d x=-\frac{1}{2} \cdot\left[\frac{2}{3}\left(1-2 x^2\right)^{\frac{3}{2}}\right]_0^{\frac{\sqrt{2}}{2}}=-\frac{1}{3} \cdot\left[\left(1-2 x^2\right)^{\frac{3}{2}}\right]_0^{\frac{\sqrt{2}}{2}}=0-\left(-\frac{1}{3}\right)=\frac{1}{3} Hence, a=3a=3. Answer: 3

Q9

Topic
5.4 Integration
Tag
Integration, Indefinite integral, Trigonometric functions
Source
M15-TZ1-P1-3(HL)
Question Text
(a) Find ∫(1+tan⁡2x)dx\int\left(1+\tan ^2 x\right) d x. [multiple choice] (a) tan⁡x+C\tan x+C (b) sec⁡x+C\sec x+C (c) 2sec⁡x⋅tan⁡x+C2 \sec x \cdot \tan x+C (d) 11+x2+C \frac{1}{1+x^2}+C
Total Mark
2
Correct Answer
a
Explanation
n/a
Mark Scheme
∫(1+tan⁡2x)dx=∫sec⁡2xdx=tan⁡x+C\int\left(1+\tan ^2 x\right) d x=\int \sec ^2 x d x=\tan x+C Answer: A
Question Text
(b) Find ∫sin⁡2xdx\int \sin ^2 x d x. [multiple choice] (a) x2−sin⁡2x4+C\frac{x}{2}-\frac{\sin 2 x}{4}+C (b) x2−sin⁡2x2+C\frac{x}{2}-\frac{\sin 2 x}{2}+C (c) 2sin⁡x⋅cos⁡x+C2 \sin x \cdot \cos x+C (d) sin⁡x⋅cos⁡x2+C\frac{\sin x \cdot \cos x}{2}+C
Total Mark
2
Correct Answer
a
Explanation
na
Mark Scheme
Use the double angle formula. sin⁡2xdx=∫1−cos⁡2x2dx=x2−sin⁡2x4+C\sin ^2 x d x=\int \frac{1-\cos 2 x}{2} d x=\frac{x}{2}-\frac{\sin 2 x}{4}+C Answer: A

Q10

Topic
5.4 Integration
Tag
Integration, Indefinite integral, Substitution, Trigonometric functions, Exponential and Logarithmic functions
Source
M15-TZ1-P1-8(HL)
Question Text
By using the substitution u=ex+2u=e^x+2, find ∫exe2x+4ex+8dx\int \frac{e^x}{e^{2 x}+4 e^x+8} d x. [multiple choice] (a) 12arctan⁡(2ex)+C\frac{1}{2} \arctan \left(2 e^x\right)+C (b) 12arctan⁡(ex+22)+C\frac{1}{2} \arctan \left(\frac{e^x+2}{2}\right)+C (c) 12arctan⁡(ex2)+C\frac{1}{2} \arctan \left(\frac{e^x}{2}\right)+C (d) 12arctan⁡(ex+2)+C\frac{1}{2} \arctan \left(e^x+2\right)+C
Total Mark
7
Correct Answer
b
Explanation
na
Mark Scheme
Integrate u:dudx=exu: \frac{d u}{d x}=e^x If we substitute uu to the equation, the integral is ∫ex(ex+2)2+22dx=∫1u2+22du\int \frac{e^x}{\left(e^x+2\right)^2+2^2} d x=\int \frac{1}{u^2+2^2} d u Then, ∫1u2+22du=12arctan⁡(u2)+C=12arctan⁡(ex+22)+C\int \frac{1}{u^2+2^2} d u=\frac{1}{2} \arctan \left(\frac{u}{2}\right)+C=\frac{1}{2} \arctan \left(\frac{e^x+2}{2}\right)+C Answer: B

Q11

Topic
5.4 Integration
Tag
Integration Indefinite Integral Definite Integral Substitution By Parts Partial Fractions Riemann Sum Trigonometric Functions Logarithmic Functions
Source
M15-TZ2-P1-5(HL)
Question Text
The value of ∫13x5ln⁡xdx\int_1^3 x^5 \ln x d x can be expressed as A2ln⁡3−B4\frac{A}{2} \ln 3-\frac{B}{4}. Find the value of A−BA-B.
Total Mark
6
Correct Answer
162
Explanation
n/a
Mark Scheme
Attempt integration by parts. Then, u=ln⁡x⇒dudx=1x/dvdx=x5⇒v=x66u=\ln x \Rightarrow \frac{d u}{d x}=\frac{1}{x} / \frac{d v}{d x}=x^5 \Rightarrow v=\frac{x^6}{6} ∫13x5ln⁡xdx=[x66ln⁡x]13−∫13x56dx=[x66ln⁡x]13−[x636]13∫13x5ln⁡xdx=2432ln⁡3−814\begin{aligned} \int_1^3 x^5 \ln x d x= & {\left[\frac{x^6}{6} \ln x\right]_1^3-\int_1^3 \frac{x^5}{6} d x=\left[\frac{x^6}{6} \ln x\right]_1^3-\left[\frac{x^6}{36}\right]_1^3 } \\ & \int_1^3 x^5 \ln x d x=\frac{243}{2} \ln 3-\frac{81}{4} \end{aligned} Since A=243A=243 and B=81,A−B=162B=81, A-B=162 Answer: 162

Q12

Topic
5.4 Integration
Tag
Integration Indefinite Integral Definite Integral Substitution By Parts Partial Fractions Riemann Sum Trigonometric Functions Logarithmic Functions Area
Source
M15-TZ2-P1-8(HL)
Question Text
By using the substitution t=tan⁡xt=\tan x, find ∫dx1+sin⁡2x\int \frac{d x}{1+\sin ^2 x}. Express your answer in the form marctan⁡(ntan⁡x)+cm \arctan (n \tan x)+c where m,nm, n are constants to be determined. Find the product of mm and nn.
Total Mark
8
Correct Answer
1
Explanation
n/a
Mark Scheme
Find the derivative of tt. t=tan⁡x⇒dtdx=sec⁡2x=1+tan⁡2x=1+t2dx=dt1+t2\begin{gathered} t=\tan x \Rightarrow \frac{d t}{d x}=\sec ^2 x=1+\tan ^2 x=1+t^2 \\ d x=\frac{d t}{1+t^2} \end{gathered} Using the fact that sin⁡x=t1+t2\sin x=\frac{t}{\sqrt{1+t^2}}, we can attempt integration by substitution. ∫dx1+sin⁡2x=∫dt1+t21+(t1+t2)2=∫dt(1+t2)+t2=∫dt1+2t2=∫dt(1+t2)+t2=∫dt1+2t2=∫dx1+sin⁡2x=12∫dt12+t2=12×112arctan⁡(t12)=22arctan⁡(2tan⁡x)+C\begin{gathered} \int \frac{d x}{1+\sin ^2 x}=\int \frac{\frac{d t}{1+t^2}}{1+\left(\frac{t}{\sqrt{1+t^2}}\right)^2} \\ =\int \frac{d t}{\left(1+t^2\right)+t^2}=\int \frac{d t}{1+2 t^2}=\int \frac{d t}{\left(1+t^2\right)+t^2}=\int \frac{d t}{1+2 t^2} \\ =\int \frac{d x}{1+\sin ^2 x}=\frac{1}{2} \int \frac{d t}{\frac{1}{2}+t^2}=\frac{1}{2} \times \frac{1}{\frac{1}{\sqrt{2}}} \arctan \left(\frac{t}{\frac{1}{\sqrt{2}}}\right) \\ =\frac{\sqrt{2}}{2} \arctan (\sqrt{2} \tan x)+C \end{gathered} Since m=22m=\frac{\sqrt{2}}{2} and n=2n=\sqrt{2}, the product of mm and nn is 1 . Answer: 1

Q13

Topic
5.4 Integration
Tag
Source
N14/5/MATHL/HP1/ENG/TZ0/XX/6
Question Text
By using the substitution u=1+xu=1+\sqrt{x}, find ∫x1+xdx\int \frac{\sqrt{x}}{1+\sqrt{x}} d x. Express your answer in x+Ax+B+Cln⁡(1+x)+Cx+A \sqrt{x}+B+C \ln (1+\sqrt{x})+C. Find the sum of A,BA, B, and CC.
Total Mark
6
Correct Answer
-3
Explanation
n/a
Mark Scheme
Find the derivative of uu. dudx=12xdx=2xdu=2(u−1)du\begin{gathered} \frac{d u}{d x}=\frac{1}{2 \sqrt{x}} \\ d x=2 \sqrt{x} d u=2(u-1) d u \end{gathered} Then, use substitution to find your answer. ∫x1+xdx=2∫(u−1)2udu=2∫u−2+1udu=u2−4u+2ln⁡u+C∫x1+xdx=x−2x−3+2ln⁡(1+x)+C\begin{gathered} \int \frac{\sqrt{x}}{1+\sqrt{x}} d x=2 \int \frac{(u-1)^2}{u} d u=2 \int u-2+\frac{1}{u} d u=u^2-4 u+2 \ln u+C \\ \int \frac{\sqrt{x}}{1+\sqrt{x}} d x=x-2 \sqrt{x}-3+2 \ln (1+\sqrt{x})+C \end{gathered} Since A=−2,B=−3,C=2,A+B+C=−3A=-2, B=-3, C=2, A+B+C=-3. Answer: -3

Q14

Topic
5.4 Integration
Tag
Differentiation Integration, Definite integral, Exponential and Logarithmic functions, Area
Source
N14/5/MATHL/HP1/ENG/TZ0/XX/11
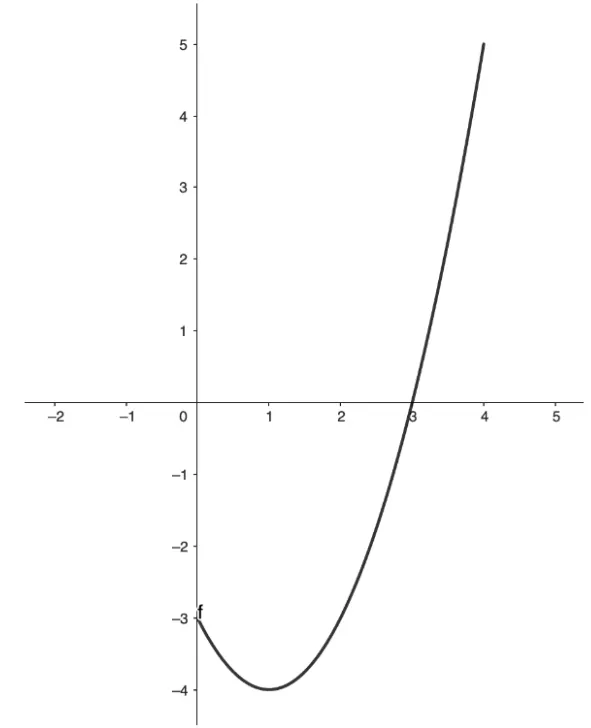
Question Text
The function gg is defined as q(x)=ln⁡x,x∈R+q(x)=\ln x, x \in R^{+}. The graph of y=q(x)y=q(x) intersects the xx-axis at the point Q . (a) Find the equation of the tangent TT to the graph of y=q(x)y=q(x) at the point Q . [multiple choice] (a) y=−x+1y=-x+1 (b) y=−x−1y=-x-1 (c) y=x−1y=x-1 (d) y=x+1y=x+1
Total Mark
3
Correct Answer
c
Explanation
n/a
Mark Scheme
Using the information that q(x)q(x) meets the x -axis at point Q , the coordinates of Q are (1,0)(1,0). To find the gradient of the tangent line, we can find the derivative of g(x)g(x). dydx=1x\frac{d y}{d x}=\frac{1}{x} At point QQ, the gradient is dydx=1\frac{d y}{d x}=1 Therefore, the equation of that tangent line is equal to y=x−1y=x-1. Answer: C
Question Text
(b) A region RR is bounded by the graphs of y=q(x)y=q(x), the tangent TT and the line x=ex=e. Find the area of the region RR. [multiple choice] (a) e2−2e−14\frac{e^2-2 e-1}{4} (b) (e−1)24\frac{(e-1)^2}{4} (c) (e+1)24\frac{(e+1)^2}{4} (d) e24\frac{e^2}{4}
Total Mark
4
Correct Answer
b
Explanation
na
Mark Scheme
Let the required area be AA. A=∫1ex−1dx−∫1eln⁡xdxA=\int_1^e x-1 d x-\int_1^e \ln x d x Attempt to use integration by parts to find ∫ln⁡xdx\int \ln x d x. A=[x22−x]1e−[xln⁡x−x]1eA=e22−e−12(e2−2e−12)=2e2−4e−e2+2e+14=(e−1)24\begin{gathered} A=\left[\frac{x^2}{2}-x\right]_1^e-[x \ln x-x]_1^e \\ A=\frac{e^2}{2}-e-\frac{1}{2}\left(\frac{e^2-2 e-1}{2}\right)=\frac{2 e^2-4 e-e^2+2 e+1}{4}=\frac{(e-1)^2}{4} \end{gathered} Answer: B

Q15

Topic
5.4 Integration
Tag
Integration, Definite integral, Trigonometric functions
Source
N14/5/MATHL/HP1/ENG/TZ0/XX/13b
Question Text
Find the value of ∫03π8cos⁡3xcos⁡3xdx\int_0^{\frac{3 \pi}{8}} \frac{\cos 3 x}{\cos ^3 x} d x. [multiple choice] (a) 3π−3−333 \pi-3-3 \sqrt{3} (b) 3π2−3−33\frac{3 \pi}{2}-3-3 \sqrt{3} (c) 3+333+3 \sqrt{3} (d) 3−333-3 \sqrt{3}
Total Mark
4
Correct Answer
b
Explanation
na
Mark Scheme
∫03π8cos⁡3xcos⁡3xdx=∫03π84cos⁡3x−3cos⁡xcos⁡3xdx=∫03π84−3sec⁡2xdx=[4x−3tan⁡x]03π8=3π2−3tan⁡3π8=3π2−3(1+3)=3π2−3−33\begin{gathered} \int_0^{\frac{3 \pi}{8}} \frac{\cos 3 x}{\cos ^3 x} d x=\int_0^{\frac{3 \pi}{8}} \frac{4 \cos ^3 x-3 \cos x}{\cos ^3 x} d x \\ =\int_0^{\frac{3 \pi}{8}} 4-3 \sec ^2 x d x \\ =[4 x-3 \tan x]_0^{\frac{3 \pi}{8}} \\ =\frac{3 \pi}{2}-3 \tan \frac{3 \pi}{8}=\frac{3 \pi}{2}-3(1+\sqrt{3}) \\ =\frac{3 \pi}{2}-3-3 \sqrt{3} \end{gathered} Answer: B

Q16

Topic
5.4 Integration
Tag
Trigonometric functions
Source
M14/5/MATHL/HP1/ENG/TZ1/X/5
Question Text
(a) Use the identity cos⁡2θ=1−2sin⁡2θ\cos 2 \theta=1-2 \sin ^2 \theta to find an expression for sin⁡12x,0≤x≤π\sin \frac{1}{2} x, 0 \leq x \leq \pi. (a) 1−cos⁡x2\sqrt{\frac{1-\cos x}{2}} (b) 1+cos⁡x2\sqrt{\frac{1+\cos x}{2}} (c) 1−cos⁡2x2\sqrt{\frac{1-\cos ^2 x}{2}} (d) 1+cos⁡2x2\sqrt{\frac{1+\cos ^2 x}{2}}
Total Mark
3
Correct Answer
a
Explanation
na
Mark Scheme
cos⁡x=1−2sin⁡212xsin⁡12x=±1−cos⁡x2\begin{aligned} & \cos x=1-2 \sin ^2 \frac{1}{2} x \\ & \sin \frac{1}{2} x= \pm \sqrt{\frac{1-\cos x}{2}} \end{aligned} positive as 0≤x≤π0 \leq x \leq \pi sin⁡12x=1−cos⁡x2\sin \frac{1}{2} x=\sqrt{\frac{1-\cos x}{2}} Answer: A
Question Text
(b) By also considering the expression for cos⁡12x\cos \frac{1}{2} x find the value of ∫0π2(1+cos⁡x2+1−cos⁡x2)dx\int_0^{\frac{\pi}{2}}\left(\sqrt{\frac{1+\cos x}{2}}+\sqrt{\frac{1-\cos x}{2}}\right) d x.
Total Mark
4
Correct Answer
2
Explanation
na
Mark Scheme
Using cos⁡2θ=2sin⁡2θ−1\cos 2 \theta=2 \sin ^2 \theta-1 cos⁡12x=1+cos⁡x2\cos \frac{1}{2} x=\sqrt{\frac{1+\cos x}{2}} Thus ∫0π2(1+cos⁡x2+1−cos⁡x2)dx=∫0π2cos⁡12x+sin⁡12xdx=[2sin⁡12x−2cos⁡12x]0π2=2−2−(0−2)=2\begin{aligned} \int_0^{\frac{\pi}{2}}\left(\sqrt{\frac{1+\cos x}{2}}\right. & \left.+\sqrt{\frac{1-\cos x}{2}}\right) d x=\int_0^{\frac{\pi}{2}} \cos \frac{1}{2} x+\sin \frac{1}{2} x d x \\ & =\left[2 \sin \frac{1}{2} x-2 \cos \frac{1}{2} x\right]_0^{\frac{\pi}{2}} \\ & =\sqrt{2}-\sqrt{2}-(0-2)=2 \end{aligned} Answer: 2

Q17

Topic
5.4 Integration
Tag
Source
M14/5/MATHL/HP1/ENG/TZ1/X/11
Question Text
Consider the function f(x)=2ln⁡xx,x>0f(x)=\frac{2 \ln x}{x}, x>0. Find the area enclosed by the curve y=f(x)\mathrm{y}=\mathrm{f}(\mathrm{x}), the line x=ex=e and the x-axis.
Total Mark
5
Correct Answer
1
Explanation
na
Mark Scheme
The x -intercept is x=1x=1 So, =∫1e2ln⁡xxdx=\int_1^e \frac{2 \ln x}{x} d x Using the substitution u=ln⁡xdudx=1xu=\ln x \\\frac{d u}{d x}=\frac{1}{x} 2∫01udu=2[u22]012 \int_0^1 u d u=2\left[\frac{u^2}{2}\right]_0^1 Answer: 1

Q18

Topic
5.4 Integration
Tag
Integration, Definite integral, Substitution, Trigonometric functions
Source
M14/5/MATHL/HP1/ENG/TZ2/XX/10
Question Text
Use the substitution x=atan⁡θx=\operatorname{atan} \theta to find an expression for ∫aa31x2x2+a2dx=124a3(33+π−6)\int_a^{a \sqrt{3}} \frac{1}{x^2 \sqrt{x^2+a^2}} d x=\frac{1}{24 a^3}(3 \sqrt{3}+\pi-6) [multiple choice] (a) 1a3\frac{1}{a^3} (b) 3−22a3\frac{3-2 \sqrt{2}}{a^3} (c) 3−2a3\frac{\sqrt{3}-\sqrt{2}}{a^3} (d) 32−233a3\frac{3 \sqrt{2}-2 \sqrt{3}}{3 a^3}
Total Mark
7
Correct Answer
d
Explanation
na
Mark Scheme
x=atan⁡θdxdθ=asec⁡2θ\begin{gathered} x=\operatorname{atan} \theta \\ \frac{d x}{d \theta}=\operatorname{asec}^2 \theta \end{gathered} new limits: x=a→θ=π4 and x=a3→θ=π3∫π4π3asec⁡2θa2tan⁡2θa2tan⁡2θ+a2dθ=∫π4a3tan⁡2θtan⁡2θ+1π3dθ=∫π4π3sec⁡2θa3tan⁡2θsec⁡θdθ=∫π4π3cos⁡θa3sin⁡2θdθ=1a3∫π4π3cot⁡θcosec⁡θdθ=−1a3[cosec⁡x]π4π3=−1a3[cosec⁡x]π4π3=−1a3(23−2)=1a3(32−233)=32−233a3\begin{aligned} & x=a \rightarrow \theta=\frac{\pi}{4} \text { and } x=a \sqrt{3} \rightarrow \theta=\frac{\pi}{3} \\ & \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \frac{a \sec ^2 \theta}{a^2 \tan ^2 \theta \sqrt{a^2 \tan ^2 \theta+a^2}} d \theta \\ & =\int_{\frac{\pi}{4} a^3 \tan ^2 \theta \sqrt{\tan ^2 \theta+1}}^{\frac{\pi}{3}} d \theta \\ & =\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \frac{\sec ^2 \theta}{a^3 \tan ^2 \theta \sec \theta} d \theta=\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \frac{\cos \theta}{a^3 \sin ^2 \theta} d \theta=\frac{1}{a^3} \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \cot \theta \operatorname{cosec} \theta d \theta \\ & =-\frac{1}{a^3}[\operatorname{cosec} x]{\frac{\pi}{4}}^{\frac{\pi}{3}}=-\frac{1}{a^3}[\operatorname{cosec} x]{\frac{\pi}{4}}^{\frac{\pi}{3}} \\ & =-\frac{1}{a^3}\left(\frac{2}{\sqrt{3}}-\sqrt{2}\right)=\frac{1}{a^3}\left(\frac{3 \sqrt{2}-2 \sqrt{3}}{3}\right)=\frac{3 \sqrt{2}-2 \sqrt{3}}{3 a^3} \end{aligned} Answer: D

Q19

Topic
5.4 Integration
Tag
Source
M14/5/MATHL/HP1/ENG/TZ2/XX/13
Question Text
The graph of the function f(x)=x−1x2+1f(x)=\frac{x-1}{x^2+1} is shown below.
Find the area of the region enclosed by the graph of y=f(x)y=f(x), the xx-axis and yy-axis.[multiple choice] (a) ln⁡2+π4\ln \sqrt{2}+\frac{\pi}{4} (b) ln⁡2+π4\ln 2+\frac{\pi}{4} (c) ln⁡2−π4\ln \sqrt{2}-\frac{\pi}{4} (d) ln⁡2−π2\ln 2-\frac{\pi}{2}
Total Mark
5
Correct Answer
c
Explanation
na
Mark Scheme
∫01x−1x2+1dx∫01x−1x2+1dx=∫01xx2+1dx−∫011x2+1dx=[12ln⁡(x2+1)−arctan⁡(x)]01=12ln⁡2−arctan⁡1−12ln⁡1+arctan⁡tan⁡(0)=ln⁡2−π4\begin{gathered} \int_0^1 \frac{x-1}{x^2+1} d x \\ \int_0^1 \frac{x-1}{x^2+1} d x=\int_0^1 \frac{x}{x^2+1} d x-\int_0^1 \frac{1}{x^2+1} d x \\ =\left[\frac{1}{2} \ln \left(x^2+1\right)-\arctan (x)\right]_0^1 \\ =\frac{1}{2} \ln 2-\arctan 1-\frac{1}{2} \ln 1+\arctan \tan (0) \\ =\ln \sqrt{2}-\frac{\pi}{4} \end{gathered} Answer: C

Q20

Topic
5.4 Integration
Tag
Functions
Source
N13-TZ0-P1-10(HL)
Question Text
The function ff is given by f(x)=x2e−x(x≥0)f(x)=x^2 e^{-x}(x \geq 0) (a) The graph of the function gg is obtained from the graph of ff by stretching it in the xx-direction by a scale factor of 3. (i) Write down an expression for g(x)g(x). [multiple choice] Options: (a) g(x)=x23e−x/3g(x)=\frac{x^2}{3} e^{-x / 3} (b) g(x)=x29e−x/3g(x)=\frac{x^2}{9} e^{-x / 3} (c) g(x)=3x2e−xg(x)=3 x^2 e^{-x} (d) g(x)=9x2e−3xg(x)=9 x^2 e^{-3 x} Total Mark : 2 Correct Answer : b Explanation : na Mark Scheme : g(x)=x29e−x/3g(x)=\frac{x^2}{9} e^{-x / 3} Answer: B (ii) State the xx-coordinate of the maximum of f(x)f(x). Total Mark : 4 Correct Answer : 2 Explanation : na Mark Scheme : As f′(x)<0f^{\prime}(x)<0 when x>2x>2, f′(x)=2xe−x−x2e−x=e−x(2−x)x=0f^{\prime}(x)=2 x e^{-x}-x^2 e^{-x}=e^{-x}(2-x) x=0 Answer: 2 (iii) Hence state the x-coordinate of the maximum of g(x)g(x) Total Mark : 1 Correct Answer : 6 Explanation : na Mark Scheme : 2 x 3 =6 Answer: 6
Question Text
(b) Find an exact value for the area of the region bounded by the curve y=g(x)y=g(x), the xx-axis and the line x=1x=1. (a) 3−e−133-e^{-\frac{1}{3}} (b) 6−23e−136-\frac{2}{3} e^{-\frac{1}{3}} (c) 3−173e−133-\frac{17}{3} e^{-\frac{1}{3}} (d) 6−373e−136-\frac{37}{3} e^{-\frac{1}{3}}
Total Mark
3
Correct Answer
d
Explanation
na
Mark Scheme
A=∫01x29e−x3dxA=\int_0^1 \frac{x^2}{9} e^{-\frac{x}{3}} d x Attempt at integration by parts twice, =[−x23e−x3]01−∫01−2x3e−x2dx=[−x23e−x3]01+[−2xe−x3]01−∫01−2e−x3dx=[−x23e−x3−2xe−x3−6e−x3]01=6−373e−13\begin{gathered} =\left[-\frac{x^2}{3} e^{-\frac{x}{3}}\right]_0^1-\int_0^1-\frac{2 x}{3} e^{-\frac{x}{2}} d x \\ =\left[-\frac{x^2}{3} e^{-\frac{x}{3}}\right]_0^1+\left[-2 x e^{-\frac{x}{3}}\right]_0^1-\int_0^1-2 e^{-\frac{x}{3}} d x \\ =\left[-\frac{x^2}{3} e^{-\frac{x}{3}}-2 x e^{-\frac{x}{3}}-6 e^{-\frac{x}{3}}\right]_0^1 \\ =6-\frac{37}{3} e^{-\frac{1}{3}} \end{gathered} Answer: D

Q21

Topic
5.4 Integration
Tag
Integration Indefinite Integral Definite Integral Substitution By Parts Partial Fractions Riemann Sum Trigonometric Functions Logarithmic Functions Area Graphs Differentiation
Source
M13-TZ1-P1-10(HL)
Question Text
(a) Find an integer value of xx for 1≤x1 \leq x such that cos⁡(πx−1)=0\cos \left(\pi x^{-1}\right)=0
Total Mark
2
Correct Answer
2
Explanation
na
Mark Scheme
cos⁡(πx−1)=0cos⁡π2=0\begin{gathered} \cos \left(\pi x^{-1}\right)=0 \\ \cos \frac{\pi}{2}=0 \end{gathered} Answer: 2
Question Text
(b) Evaluate ∫0.52∣πx−2cos⁡(πx−1)∣dx\int_{0.5}^2\left|\pi x^{-2} \cos \left(\pi x^{-1}\right)\right| d x.
Total Mark
2
Correct Answer
1
Explanation
na
Mark Scheme
Take the substitution u=πx−1,dudx=−πx−2u=\pi x^{-1}, \frac{d u}{d x}=-\pi x^{-2} and change the limits ∫2ππ21−cos⁡(u)∣ du∣[−sin⁡(u)]2ππ2∣∣−1−0∣=1\begin{aligned} & \left.\int_{2 \pi}^{\frac{\pi}{2}} 1-\cos (u) \right\rvert\, d u \\ & \left|[-\sin (u)]_{2 \pi}^{\frac{\pi}{2}}\right| \\ & |-1-0|=1 \end{aligned} Answer: 1

Q22

Topic
5.4 Integration
Tag
Integration Indefinite Integral Definite Integral Substitution By Parts Partial Fractions Riemann Sum Trigonometric Functions Logarithmic Functions Area Graphs Differentiation Limits
Source
M13-TZ1-P1-12(HL)
Question Text
(a) 3x2−6x+63 x^2-6 x+6 can be written in the form a(x−h)2+ka(x-h)^2+k where a,h,k∈Z+a, h, k \in Z^{+}Find the value of a+h+ka+h+k
Total Mark
2
Correct Answer
7
Explanation
na
Mark Scheme
3(x−1)2+33(x-1)^2+3 Answer: 7
Question Text
(b) The function ff is defined by f(x)=13x2−6x+6f(x)=\frac{1}{3 x^2-6 x+6} Which is the range of ff can be written as 0<f(x)<1n0<f(x)<\frac{1}{n} where n∈Z+n \in Z^{+}. Find the value of nn.
Total Mark
2
Correct Answer
3
Explanation
na
Mark Scheme
The minimum value of 3(x−1)2+33(x-1)^2+3 is 3 , thus the maximum value of 13x2−6x+6\frac{1}{3 x^2-6 x+6} is 13\frac{1}{3}. Answer: 3
Question Text
(c) The value of ∫1.5414x2−4x+5dx=πm\int_{1.5}^4 \frac{1}{4 x^2-4 x+5} d x=\frac{\pi}{m} where m∈Z+m \in Z^{+}. By suing a suitable substitution, solve the integral to find the value of m⋅[7]m \cdot[7]
Total Mark
7
Correct Answer
12
Explanation
na
Mark Scheme
Using the substitution u=x−1,dudx=1u=x-1, \frac{d u}{d x}=1, and redefining the limits, ∫0.5313u2+3du=13[arctan⁡(u)]0.53=13(arctan⁡3−arctan⁡0.5)\int_{0.5}^3 \frac{1}{3 u^2+3} d u=\frac{1}{3}[\arctan (u)]{0.5}^3=\frac{1}{3}(\arctan 3-\arctan 0.5) Using the compound angle identity for tan tan⁡(arctan⁡(3)−arctan⁡(12))=3−121+12×3=1\tan \left(\arctan (3)-\arctan \left(\frac{1}{2}\right)\right)=\frac{3-\frac{1}{2}}{1+\frac{1}{2} \times 3}=1 So, arctan⁡(3)−arctan⁡(12)=arctan⁡(1)=π4\arctan (3)-\arctan \left(\frac{1}{2}\right)=\arctan (1)=\frac{\pi}{4} Thus, ∫0.5313u2+3du=π12\int{0.5}^3 \frac{1}{3 u^2+3} d u=\frac{\pi}{12} Answer: 12

Q23

Topic
5.4 Integration
Tag
Integration, Definite integral, Trigonometric functions, Exponential and Logarithmic functions
Source
M13-TZ2-P1-1(HL)
Question Text
Find the exact value of ∫12((x−1)2+1x+cos⁡πx)dx\int_1^2\left((x-1)^2+\frac{1}{x}+\cos \pi x\right) d x. (a) =3+ln⁡2=3+\ln 2 (b) =1+ln⁡2+1π=1+\ln 2+\frac{1}{\pi} (c) =13+ln⁡2=\frac{1}{3}+\ln 2 (d) =13+ln⁡2−2π=\frac{1}{3}+\ln 2-\frac{2}{\pi}
Total Mark
6
Correct Answer
c
Explanation
na
Mark Scheme
[13(x−1)3+ln⁡x+1πsin⁡πx]12=(13+ln⁡2+1πsin⁡2π)−(0+ln⁡1+1πsin⁡π)=13+ln⁡2\begin{gathered} {\left[\frac{1}{3}(x-1)^3+\ln x+\frac{1}{\pi} \sin \pi x\right]_1^2} \\ =\left(\frac{1}{3}+\ln 2+\frac{1}{\pi} \sin 2 \pi\right)-\left(0+\ln 1+\frac{1}{\pi} \sin \pi\right) \\ =\frac{1}{3}+\ln 2 \end{gathered} Answer: C

Q24

Topic
5.4 Integration
Tag
Source
N19/5/MATHL/HP1/ENG/TZ1/XX/2
Question Text
Given that ∫0ln⁡ke3xdx=21\int_0^{\ln k} e^{3 x} d x=21, find the value of kk.
Total Mark
5
Correct Answer
4
Explanation
na
Mark Scheme
Solve the integral [13e3x]0ln⁡k=13e3ln⁡k−13e013k3−13=21k3=64k=4\begin{gathered} {\left[\frac{1}{3} e^{3 x}\right]_0^{\ln k}=\frac{1}{3} e^{3 \ln k}-\frac{1}{3} e^0} \\ \frac{1}{3} k^3-\frac{1}{3}=21 \\ k^3=64 \\ k=4 \end{gathered} Answer: 4

Q25

Topic
5.4 Integration
Tag
Source
N19/5/MATHL/HP1/ENG/TZ1/XX/7
Question Text
(a) Write −x2+4x−3-x^2+4 x-3 in the form −a(x−h)2+k-a(x-h)^2+k where a,h,k∈Za, h, k \in Z Find the value of a+h+ka+h+k.
Total Mark
2
Correct Answer
4
Explanation
na
Mark Scheme
−x2=−(x−2)2+1a=1,h=2,k=1\begin{gathered} -x^2=-(x-2)^2+1 \\ a=1, h=2, k=1 \end{gathered} Answer: 4
Question Text
(b) Hence, find the value of ∫32521−x2+4x−3dx\int_{\frac{3}{2}}^{\frac{5}{2}} \frac{1}{\sqrt{-x^2+4 x-3}} d x. [multiple choice] (a) π12\frac{\pi}{12} (b) π6\frac{\pi}{6} (c) π4\frac{\pi}{4} (d) π3\frac{\pi}{3}
Total Mark
5
Correct Answer
d
Explanation
na
Mark Scheme
Rewrite the integral with the identity found previously, ∫325211−(x−2)2dx\int_{\frac{3}{2}}^{\frac{5}{2}} \frac{1}{\sqrt{1-(x-2)^2}} d x Using the substitution, u=x−2,dudx=1u=x-2, \frac{d u}{d x}=1 and redefining limits, ∫−121211−u2dx=[arcsin⁡(u)]−1212=arcsin⁡(12)−arcsin⁡(−12)=π6−(−π6)=π3\begin{gathered} \int_{-\frac{1}{2}}^{\frac{1}{2}} \frac{1}{\sqrt{1-u^2}} d x=[\arcsin (u)]_{-\frac{1}{2}}^{\frac{1}{2}} \\ =\arcsin \left(\frac{1}{2}\right)-\arcsin \left(-\frac{1}{2}\right) \\ =\frac{\pi}{6}-\left(-\frac{\pi}{6}\right) \\ =\frac{\pi}{3} \end{gathered} Answer: D

Q26

Topic
5.4 Integration
Tag
Source
M19/5/MATHL/HP1/ENG/TZ1/XX/9
Question Text
(a) Find an expression for (cos⁡x−sin⁡x)2(\cos x-\sin x)^2. (a) cos⁡2x\cos 2 x (b) sin⁡2x\sin 2 x (c) 1+cos⁡2x1+\cos 2 x (d) 1−sin⁡2x1-\sin 2 x
Total Mark
2
Correct Answer
d
Explanation
na
Mark Scheme
(cos⁡x−sin⁡x)2=sin⁡2x−2sin⁡xcos⁡x+cos⁡2x=1−sin⁡2x\begin{aligned} (\cos x-\sin x)^2 & =\sin ^2 x-2 \sin x \cos x+\cos ^2 x \\ & =1-\sin 2 x \end{aligned} Answer: D
Question Text
(b) Find an expression for sec⁡2x−tan⁡2x\sec 2 x-\tan 2 x. (a) cos⁡x+sin⁡xcos⁡x−sin⁡x\frac{\cos x+\sin x}{\cos x-\sin x} (b) cos⁡x−sin⁡xcos⁡x+sin⁡x\frac{\cos x-\sin x}{\cos x+\sin x} (c) 1cos⁡x+sin⁡x\frac{1}{\cos x+\sin x} (d) 1cos⁡x−sin⁡x\frac{1}{\cos x-\sin x}
Total Mark
4
Correct Answer
b
Explanation
na
Mark Scheme
sec⁡2x−tan⁡2x=1cos⁡2x−sin⁡2xcos⁡2x=1−sin⁡2xcos⁡2x=(cos⁡x−sin⁡x)2cos⁡2x−sin⁡2x=(cos⁡x−sin⁡x)2(cos⁡x−sin⁡x)(cos⁡x+sin⁡x)=cos⁡x−sin⁡xcos⁡x+sin⁡x\begin{gathered} \sec 2 x-\tan 2 x=\frac{1}{\cos 2 x}-\frac{\sin 2 x}{\cos 2 x} \\ =\frac{1-\sin 2 x}{\cos 2 x}=\frac{(\cos x-\sin x)^2}{\cos ^2 x-\sin ^2 x} \\ =\frac{(\cos x-\sin x)^2}{(\cos x-\sin x)(\cos x+\sin x)}=\frac{\cos x-\sin x}{\cos x+\sin x} \end{gathered} Answer: B
Question Text
(c) Hence or otherwise, given that ∫0π6(sec⁡2x−tan⁡2x)dx\int_0^{\frac{\pi}{6}}(\sec 2 x-\tan 2 x) d x can be written in the form ln⁡(a+b2)\ln \left(\frac{a+\sqrt{b}}{2}\right) where a,b∈Z+a, b \in Z^{+}, find the value of a+ba+b .
Total Mark
7
Correct Answer
4
Explanation
na
Mark Scheme
Using sec⁡2x−tan⁡2x=cos⁡x−sin⁡xcos⁡x+sin⁡x\sec 2 x-\tan 2 x=\frac{\cos x-\sin x}{\cos x+\sin x} ∫0π6(cos⁡x−sin⁡xcos⁡x+sin⁡x)dx=[ln⁡(cos⁡x+sin⁡x)]0π6=ln⁡(cos⁡π6+sin⁡π6)−ln⁡(cos⁡0+sin⁡0)=ln⁡(32+12)−ln⁡(1)=ln⁡3+12\begin{gathered} \int_0^{\frac{\pi}{6}}\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right) d x=[\ln (\cos x+\sin x)]_0^{\frac{\pi}{6}} \\ =\ln \left(\cos \frac{\pi}{6}+\sin \frac{\pi}{6}\right)-\ln (\cos 0+\sin 0) \\ =\ln \left(\frac{\sqrt{3}}{2}+\frac{1}{2}\right)-\ln (1) \\ =\ln \frac{\sqrt{3}+1}{2} \end{gathered} Answer: 4

Q27

Topic
5.4 Integration
Tag
Source
M19/5/MATHL/HP1/ENG/TZ1/XX/8
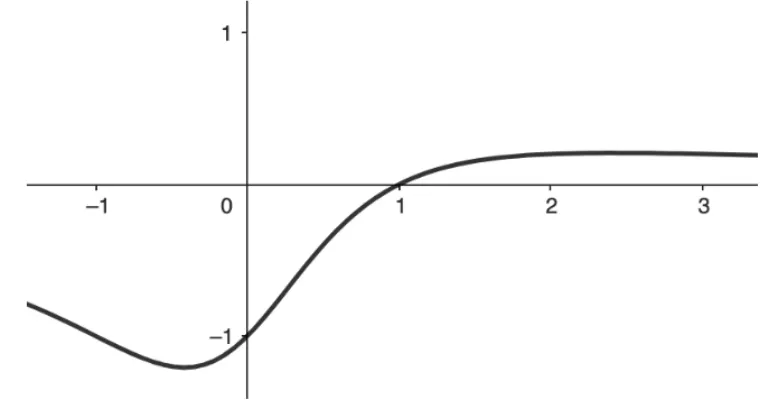
Question Text
The graph of y=f′(x),0≤x≤4y=f^{\prime}(x), 0 \leq x \leq 4 is shown in the following diagram. The curve intersects the x -axis at (3,0)(3,0) and has a local minimum at (1,−4)(1,-4)
The area enclosed by the curve y=f′(x)y=f^{\prime}(x) the xx-axis and the yy-axis is 9 . Given that f(3)=−1f(3)=-1. (a) Find the value of f(0)f(0).
Total Mark
3
Correct Answer
8
Explanation
na
Mark Scheme
Write in integral form, and as the area is under the xx-axis, the area becomes negative, ∫03f′(x)dx=−9f(3)−f(0)=−9f(0)=9−1=8\begin{gathered} \int_0^3 f^{\prime}(x) d x=-9 \\ f(3)-f(0)=-9 \\ f(0)=9-1=8 \end{gathered} Answer: 8
Question Text
The area enclosed by the curve y=f′(x)y=f^{\prime}(x) and the xx-axis between x=0x=0 and x=1x=1 is 113\frac{11}{3}. (b) The value of f(1)f(1) can be written as ab\frac{a}{b} where a,ba, b are positive integers in lowest terms. Find the value of a+ba+b.
Total Mark
2
Correct Answer
16
Explanation
na
Mark Scheme
Write in integral form, and as the area is under the x -axis, the area becomes negative, ∫01f′(x)dx=−113f(1)−f(0)=−2.5f(1)=−113+8=133\begin{gathered} \int_0^1 f^{\prime}(x) d x=-\frac{11}{3} \\ f(1)-f(0)=-2.5 \\ f(1)=-\frac{11}{3}+8=\frac{13}{3} \end{gathered} Answer: 16

Q28

Topic
5.4 Integration
Tag
Integration, Indefinite integral, Substitution, Trigonometric functions
Source
M19/5/MATHL/HP1/ENG/TZ2/XX/4
Question Text
Using the substitution u=cos⁡xu=\cos x, find ∫sin⁡3xdxcos⁡x\int \frac{\sin ^3 x d x}{\sqrt{\cos x}}. [multiple choice] (a) 25(sin⁡x)5−2sin⁡x+c\frac{2}{5}(\sqrt{\sin x})^5-2 \sqrt{\sin x}+c (b) 25(cos⁡x)5−2cos⁡x+c\frac{2}{5}(\sqrt{\cos x})^5-2 \sqrt{\cos x}+c (c) 52(sin⁡x)5−12sin⁡x+c\frac{5}{2}(\sqrt{\sin x})^5-\frac{1}{2} \sqrt{\sin x}+c (d) 52(cos⁡x)5−12cos⁡x+c\frac{5}{2}(\sqrt{\cos x})^5-\frac{1}{2} \sqrt{\cos x}+c
Total Mark
5
Correct Answer
b
Explanation
na
Mark Scheme
Using u=cos⁡x,dudx=−sin⁡xu=\cos x, \frac{d u}{d x}=-\sin x ∫sin⁡3xcos⁡xdx=∫−sin⁡2xudu=∫u2−1udu=∫(u32−u−12)du\begin{aligned} \int \frac{\sin ^3 x}{\sqrt{\cos x}} d x & =\int \frac{-\sin ^2 x}{\sqrt{u}} d u=\int \frac{u^2-1}{\sqrt{u}} d u \\ & =\int\left(u^{\frac{3}{2}}-u^{-\frac{1}{2}}\right) d u \end{aligned} =25u52−2u12+c=25(cos⁡x)5−2cos⁡x+c\begin{gathered} =\frac{2}{5} u^{\frac{5}{2}}-2 u^{\frac{1}{2}}+c \\ =\frac{2}{5}(\sqrt{\cos x})^5-2 \sqrt{\cos x}+c \end{gathered} Answer: B

Q29

Topic
5.4 Integration
Tag
Source
M18/5/MATHL/HP1/ENG/TZ1/XX/4 a,b
Question Text
Given that ∫−33f(x)dx=12\int_{-3}^3 f(x) d x=12 and ∫03f(x)dx=7\int_0^3 f(x) d x=7, find (a) ∫−30(f(x)+1)dx\int_{-3}^0(f(x)+1) d x
Total Mark
4
Correct Answer
8
Explanation
na
Mark Scheme
∫−30f(x)+1dx=∫−30f(x)dx+∫−301dx∫−30f(x)dx=∫−33f(x)dx−∫03f(x)dx=12−7=5∫−301dx=[x]−30=3\begin{gathered} \int_{-3}^0 f(x)+1 d x=\int_{-3}^0 f(x) d x+\int_{-3}^0 1 d x \\ \int_{-3}^0 f(x) d x=\int_{-3}^3 f(x) d x-\int_0^3 f(x) d x=12-7=5 \\ \int_{-3}^0 1 d x=[x]{-3}^0=3 \end{gathered} So, ∫−30f(x)+1dx=5+3=8\int{-3}^0 f(x)+1 d x=5+3=8 Answer: 8
Question Text
(b) ∫−30f(x+3)dx\int_{-3}^0 f(x+3) d x
Total Mark
2
Correct Answer
7
Explanation
na
Mark Scheme
∫−30f(x+3)dx=∫03f(x)dx=7\int_{-3}^0 f(x+3) d x=\int_0^3 f(x) d x=7 Answer: 7

Q30

Topic
5.4 Integration
Tag
Source
M18/5/MATHL/HP1/ENG/TZ1/XX/7
Question Text
Let y=arccos⁡(x4)y=\arccos \left(\frac{x}{4}\right) (a) Find dydx\frac{d y}{d x}. [multiple choice] (a) 116−x2\frac{1}{\sqrt{16-x^2}} (b) 14−x2\frac{1}{\sqrt{4-x^2}} (c) −116−x2-\frac{1}{\sqrt{16-x^2}} (d) −14−x2-\frac{1}{\sqrt{4-x^2}}
Total Mark
2
Correct Answer
c
Explanation
na
Mark Scheme
y=arccos⁡(x4)⇒dydx=−131−(x4)2=−116−x2y=\arccos \left(\frac{x}{4}\right) \Rightarrow \frac{d y}{d x}=-\frac{1}{3 \sqrt{1-\left(\frac{x}{4}\right)^2}}=-\frac{1}{\sqrt{16-x^2}} Answer: C
Question Text
(b) Find ∫02arccos⁡(x4)d\int_0^2 \arccos \left(\frac{x}{4}\right) d [multiple choice] (a) 23+42 \sqrt{3}+4 (b) π3−4\frac{\pi}{3}-4 (c) 4−234-2 \sqrt{3} (d) π3−23+4\frac{\pi}{3}-2 \sqrt{3}+4
Total Mark
7
Correct Answer
d
Explanation
na
Mark Scheme
Integration by parts u=arccos⁡(x4),dudx=−116−x2,dvdx=1,v=xu=\arccos \left(\frac{x}{4}\right), \frac{d u}{d x}=-\frac{1}{\sqrt{16-x^2}}, \frac{d v}{d x}=1, v=x Integration by inspection, ∫02arccos⁡(x4)dx=[xarccos⁡(x4)]02+∫02x16−x2dx\int_0^2 \arccos \left(\frac{x}{4}\right) d x=\left[\operatorname{xarccos}\left(\frac{x}{4}\right)\right]_0^2+\int_0^2 \frac{x}{\sqrt{16-x^2}} d x [xarccos⁡(x4)]02+[−16−x2]02=π3−23+4\begin{gathered} {\left[\operatorname{xarccos}\left(\frac{x}{4}\right)\right]_0^2+\left[-\sqrt{16-x^2}\right]_0^2} \\ =\frac{\pi}{3}-2 \sqrt{3}+4 \end{gathered} Answer: D

Q31

Topic
5.4 Integration
Tag
Source
M18/5/MATHL/HP1/ENG/TZ2/XX/6
Question Text
Consider the functions f,gf, g, defined for x∈Rx \in R, given by f(x)=e2xsin⁡xf(x)=e^{2 x} \sin x and g(x)=e2xcos⁡xg(x)=e^{2 x} \cos x. (a) Find (i) f′(x)f^{\prime}(x); [multiple choice] (a) e2xsin⁡x+e2xcos⁡xe^{2 x} \sin x+e^{2 x} \cos x (b) e2xsin⁡x−e2xcos⁡xe^{2 x} \sin x-e^{2 x} \cos x (c) 2e2xsin⁡x+2e2xcos⁡x2 e^{2 x} \sin x+2 e^{2 x} \cos x (d) 2e2xsin⁡x−2e2xcos⁡x2 e^{2 x} \sin x-2 e^{2 x} \cos x Total Mark : 3 Correct Answer : c Explanation : na Mark Scheme : Attempt at product rule f′(x)=2e2xsin⁡x+2e2xcos⁡xf^{\prime}(x)=2 e^{2 x} \sin x+2 e^{2 x} \cos x Answer: C (ii) g′(x)g^{\prime}(x) Options: (a) e2xcos⁡x+e2xsin⁡xe^{2 x} \cos x+e^{2 x} \sin x (b) e2xcos⁡x−e2xsin⁡xe^{2 x} \cos x-e^{2 x} \sin x (c) 2e2xcos⁡x+2e2xsin⁡x2 e^{2 x} \cos x+2 e^{2 x} \sin x (d) 2e2xcos⁡x−2e2xsin⁡x2 e^{2 x} \cos x-2 e^{2 x} \sin x Total Mark : 3 Correct Answer : d Explanation : na Mark Scheme : g′(x)=2e2xcos⁡x−2e2xsin⁡xg^{\prime}(x)=2 e^{2 x} \cos x-2 e^{2 x} \sin x Answer: D
Question Text
(b) Hence find ∫−π0e2xcos⁡xdx\int_{-\pi}^0 e^{2 x} \cos x d x. [multiple choice] (a) e2π2\frac{e^{2 \pi}}{2} (b) e2π+12\frac{e^{2 \pi}+1}{2} (c) e−2π2\frac{e^{-2 \pi}}{2} (d) e−2π+12\frac{e^{-2 \pi}+1}{2}
Total Mark
4
Correct Answer
a
Explanation
na
Mark Scheme
Attempt to add f′(x)f^{\prime}(x) and g′(x)g^{\prime}(x) f′(x)+g′(x)=4e2xcos⁡x∫0πe2xcos⁡xdx=14[e2xsin⁡x+e2xcos⁡x]−π014(2e2π)=e2π2\begin{gathered} f^{\prime}(x)+g^{\prime}(x)=4 e^{2 x} \cos x \\ \int_0^\pi e^{2 x} \cos x d x=\frac{1}{4}\left[e^{2 x} \sin x+e^{2 x} \cos x\right]_{-\pi}^0 \\ \frac{1}{4}\left(2 e^{2 \pi}\right)=\frac{e^{2 \pi}}{2} \end{gathered} Answer: A
N14/5/MATHL/HP1/ENG/TZ0/XX/13b
N14/5/MATHL/HP1/ENG/TZ0/XX/13b