home
Mission
//////
home
//////

A.5 Galilean and Special Relativity

생성일
2024/07/05 08:15
태그

A.5.1 Frames of reference

Frames of reference
•
The concept of position and coordinates requires one to choose an origin point as (0,0)
•
The choice of origin point does not affect any of the behaviour. This means that regardless of origin, displacement and velocity are not affected.
•
A frame of reference performs all calculations using a specific choice of point of origin (0,0), but from another observer’s perspective that point of origin can appear to be moving at a constant velocity.
•
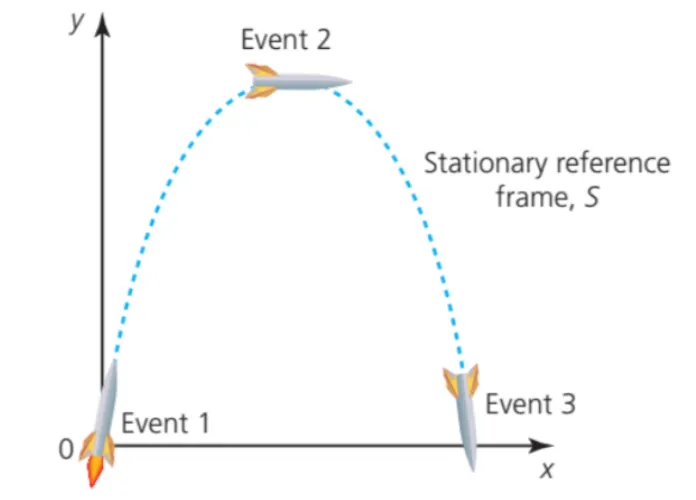
Take for example two people standing on two platforms.
◦
Each platform is able to either remain perfectly still or move at a constant velocity, and is covered in a way that nothing in the outside world is visible.
◦
Neither person is able to feel or measure if they are moving or not, so from their own perspective, they are not moving and it feels like it is the other platform and person who are moving.
◦
The difference is that each of these perspectives is a different frame of reference.
•
Once one chooses a specific frame of reference, all other frames of reference appear to have an initial position and a constant velocity.
•
There is no “correct” frame of reference. The laws of physics work the same way regardless of which frame you choose as long as all measurements are made using the same frame.
•
This is why measurements of velocity and position don’t really make sense unless one also specifies which frame of reference (point of origin) is used to make the measurements of velocity and position.
◦
Velocity of object x relative to object y, means that the velocity of x was measured using object y as the frame of reference (assume y has velocity of zero and initial position of zero)
◦
An inertial frame of reference simply means that the frame of reference being used does not accelerate
A.5.1-1 Graphical representation of the Earth’s reference frame for a rocket in flight

A.5.2 Galilean relativity

Galilean relativity
•
Galilean relativity makes sure that Newton’s laws of motion apply the same way in all frames of reference.
•
The measurement of time is the same for all frames of reference.
◦
It is assumed that one second is the same length for everyone regardless of their frame of reference, velocity or acceleration.
Galilean transformations
•
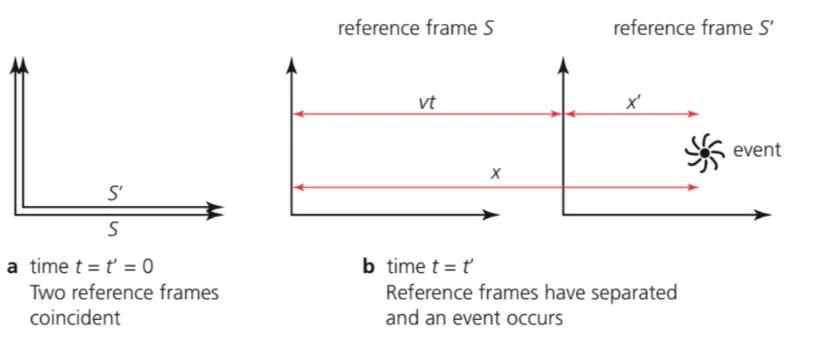
In one frame of reference the position and velocity of an object at rest relative to that object are xx and u=0 u=0 respectively.
•
Now imagine there is a second frame of reference moving at a velocity of vv relative to the first frame of reference.
•
Initial conditions
◦
First, let's set the initial position and time of both frames so that at a time t=0t=0 in the first frame, the time in the second frame t′=0 t'=0. This makes sure that both frames always have the same value of time so t=t′. t=t'.
◦
Next, the initial position of the object at t=0t=0 in the first frame of reference is x and at the same time t′=0t'=0, the position of the object relative to the second frame of reference is x′=xx'=x.
◦
Essentially, making both frames of reference start at the same time and place simplifies the formulas for later, but is not strictly necessary.
•
In the first frame of reference the object will remain at position xx at all times, but since the second frame of reference is moving towards the right at a velocity v relative to the first frame, it will appear as if everything in the first frame is moving to the left.
•
In the second frame the position of the object will be x′=x−vt x'=x-vt, since it appears to be moving towards the left at a constant velocity v.v.
•
If the object in the has an initial velocity of u u relative to the first frame of reference, it will have a position ofx=x0+ut x=x_0+ut in the first frame of reference
•
In the second frame of reference, the position of the object will appear to be x′=x0+ut−vtorx′=x0+(u−v)tx'=x_0+ut-vt or x'=x_0+(u-v)t
•
In conclusion the apparent velocity of the object in the second frame of reference will be u′=u−vu' = u-v
•
One conclusion of Galilean relativity was that the speed of light would be different for all frames of reference, and therefore an ‘absolute frame of reference’ must exist where the speed of light is the same in all directions.

A.5.3 Special relativity

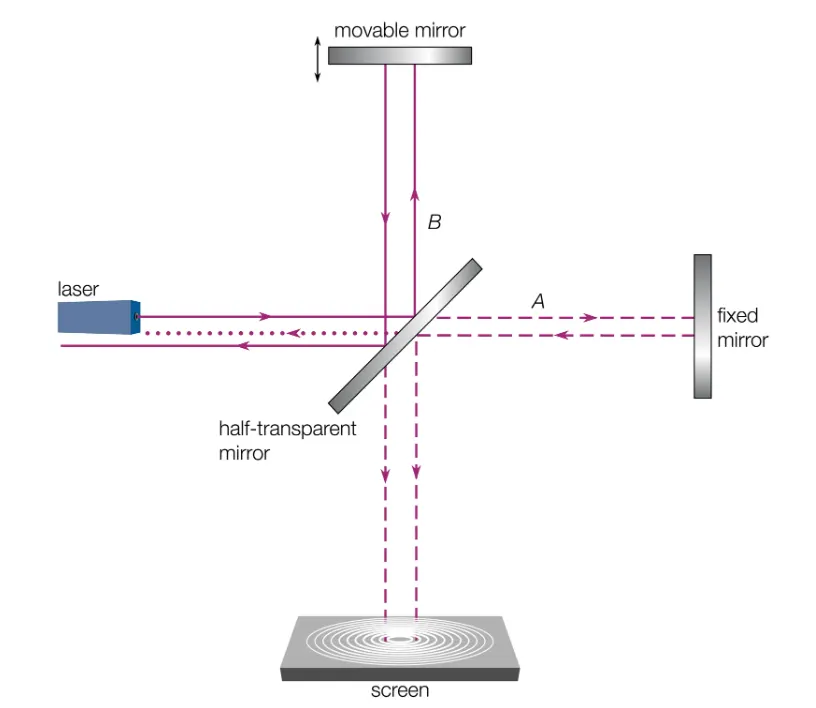
The Michelson–Morley experiment
•
The Michelson–Morley experiment is technically not required by the IB, but is important because it is one of the pieces of evidence that indicated that Galilean relativity might not be completely correct.
•
In this experiment the speed of light in perpendicular directions was measured.
•
Predictably, the speed of light was found to be the same regardless of the orientation and the frame of reference of the experiment.
◦
Changing the velocity or direction of the frame of reference of the experiment had no effect on the measurements of the speed of light!
Postulates of special relativity
•
Special relativity is a specific case within general relativity where acceleration is zero and the effects due to gravity are not considered.
◦
Special relativity is the simplified case since a=0a=0, while general relativity is more complex because the effects of acceleration and gravity need to be accounted for.
•
The first postulate of special relativity is that the laws of physics are the same in all inertial frames of reference.
•
The second postulate of special relativity is that the speed of light is the same for all inertial frames of reference.
•
Notice that although the second postulate seems reasonable, it would be impossible using Galilean transformations and Newtonian laws.
◦
Using Galilean transformations, if one person measures the speed of light to be cc, then in another frame of reference moving at a velocity of vv relative to the first; the speed of light in the second frame should be measured to be c′=c−vc'=c-v
•
The only way this is possible is that time does not pass at the same rate in different frames of reference.
◦
Recall that for Galilean relativity t=t′t=t'
◦
In special relativity t≠t′t \neq t'

A.5.4 Lorentz transformations

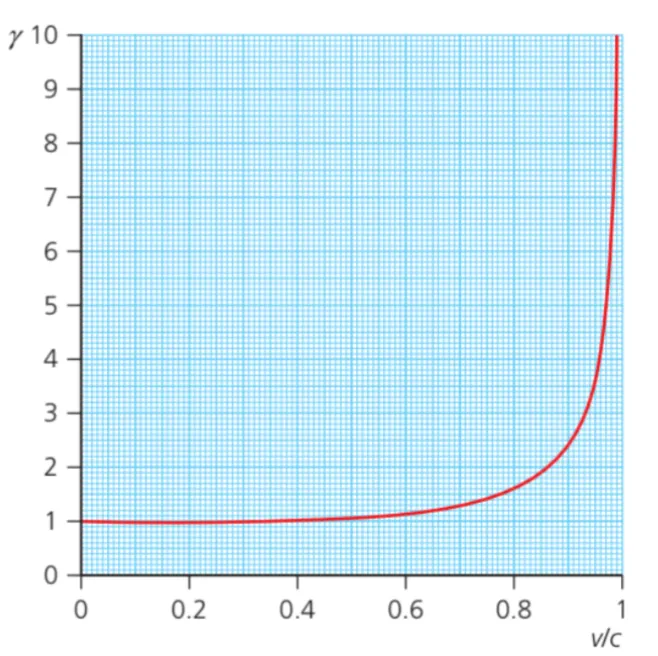
Lorentz factor
•
γ=11−v2c2\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}
A.5.4-1
Lorentz transform
•
x′=γ(x−vt)x' = \gamma (x - v t)
•
t′=γ(t−vxc2)t' = \gamma \left( t - \frac{v x}{c^2} \right)
•
u′=u−v1−uvc2u' = \frac{u - v}{1 - \frac{uv}{c^2}}

A.5.5 Space-time diagram

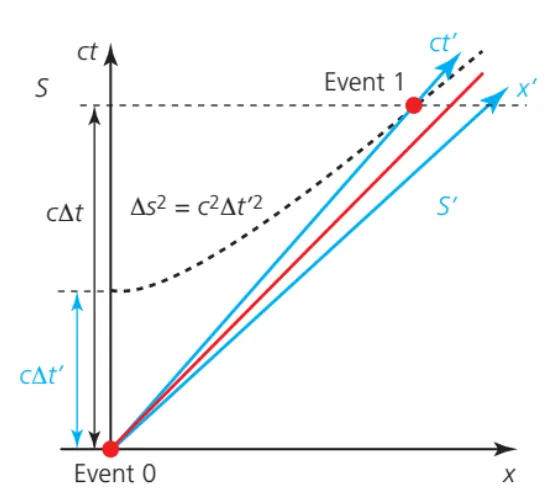
Space-time interval
•
(Δs)2=(cΔt)2−(Δx)2(\Delta s)^2 = (c \Delta t)^2 - (\Delta x)^2
Proper time
•
Δt0=Δtγ\Delta t_0 = \frac{\Delta t}{\gamma}
Proper length
•
Δt0=Δtγ\Delta t_0 = \frac{\Delta t}{\gamma}
Simultaneity
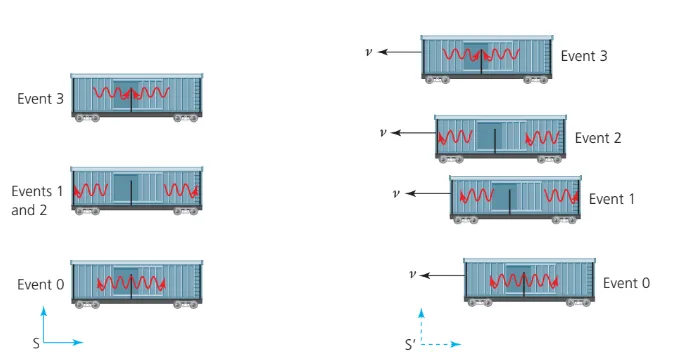
A.5.5-1 Simultaneous and non-simultaneous events
Space-time diagrams
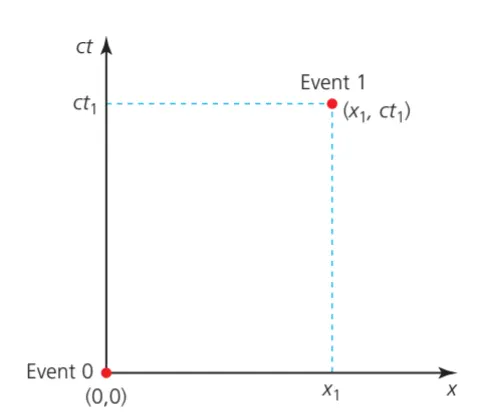
A.5.5-2 Space-time diagram for an inertial reference frame, S, showing two events and their coordinates
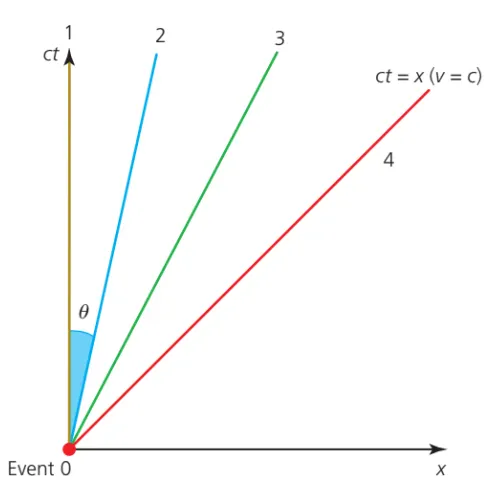
Angle of the world line
A.5.5-3 Straight world lines
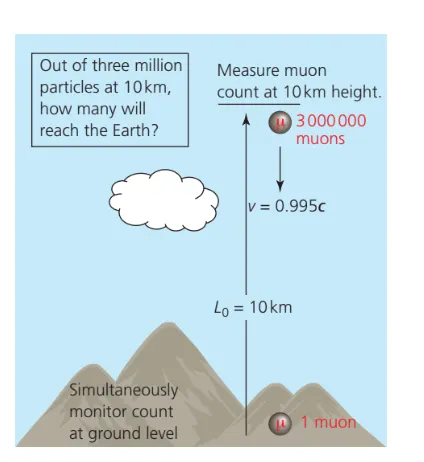
Muon decay experiments
A.5.5-4 Using classical physics to predict muon on Earth’s surface