2.3 Transformation

Topic	2.3 Transformation
Tag	Transformation; Functions; Domain Range; Asymptotes; Graph; Reflection; Scale factor; Translation; Stretch;
Source	M17/5/MATHL/HP1/ENG/TZ1/XX/6
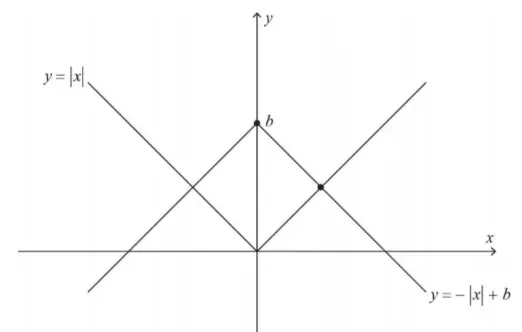
Question Text	Consider the graphs of $y=\|x\|$ and $y=-\|x\|+b$ , where $b \in Z+$ . Given that the graphs enclose a region of area 8 square units, find the value of $b$ .
Total Mark	5
Correct Answer	4
Explanation	n/a
Mark Scheme	Step 1: Consider what's given In this case, sketching the graph to visualize the given equation helps.

Mark Scheme

Important thing to note is that when

x<0,|x|=-x

and when

x>0,|x|=x

, thus the graph flips once

x

becomes positive. Step 2: Combine the given information Combine the given area, and the area found using the equations (i.e. use the variable

b

) As the area enclosed looks like two symmetrical triangles, the base length and the height should be found. Base length

=b

The coordinate of the intersection

-x+b=x

, so

x=\frac{b}{2}

Height

=\frac{b}{2}

Area enclosed

=2 \times \frac{1}{2} \times b \times \frac{b}{2}=\frac{b^2}{2}=8

So

b=4

Topic	2.3 Transformation
Tag	Transformation; Functions; Domain Range; Asymptotes; Graph; Reflection; Scale factor; Translation; Stretch;
Source	M17/5/MATHL/HP1/ENG/TZ1/XX/11 b,e
Question Text	Consider the function $f(x)=\frac{1}{x^2-3 x+2}, x \in R, x \neq 2, x \neq 1.$ Sketch the graph of $y=f(\|x\|)$

Total Mark	4
Correct Answer	(b)
Explanation	n/a
Mark Scheme	As $f(-x)=f(x)$ the function should be symmetrical across the $y$ -axis. The graph of $f(\|x\|)$ where $x<0$ is the mirror image of $f(x)$ where $x>0$ .

Topic	2.3 Transformation
Tag	Transformation; Functions; Domain Range; Asymptotes; Graph; Reflection; Scale factor; Translation; Stretch;
Source	M17/5/MATHL/HP1/ENG/TZ2/XX/9
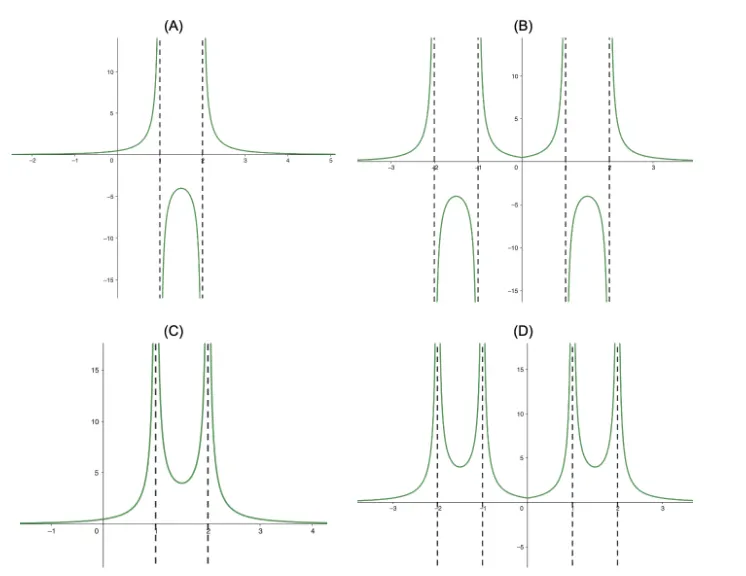
Question Text	Consider the function $f(x)=x^2-a^2, x \in R$ where $a$ is a positive constant. Graph the equation $y=\left\|\frac{1}{f(x)}\right\|$ .

Total Mark	5
Correct Answer	(a)
Explanation	n/a
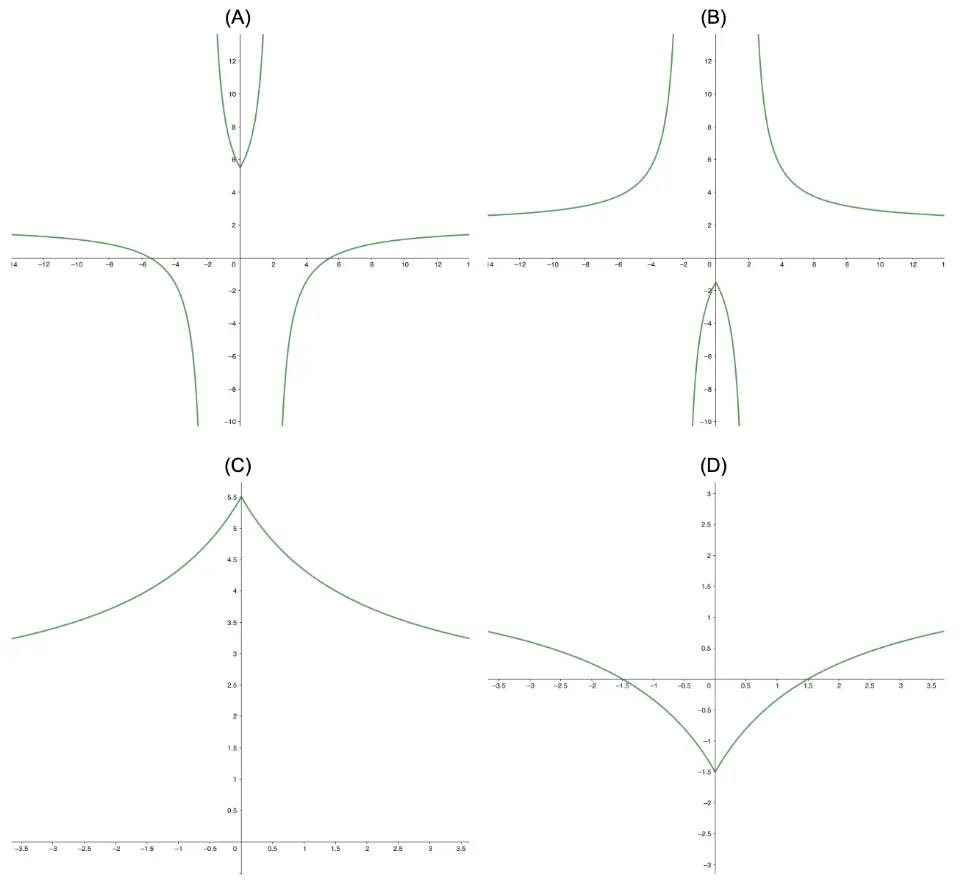
Mark Scheme	Graph is symmetrical across the $y$ -axis, and is above the $x$ -axis. The graph has two vertical asymptotes $x=a, x=-a.$

Topic	2.3 Transformation
Tag	Transformation; Functions; Domain Range; Asymptotes; Graph; Reflection; Scale factor; Translation; Stretch;
Source	M15-TZ1-P1-9(HL)
Question Text	The functions $f$ and $g$ are defined by $f(x)=3 x+\frac{\pi}{4}, x \in R$ and $g(x)=2 \sin x+3, x \in R$ . (a) The range $g \circ f(x)$ can be written as $a \leq g \circ f(x) \leq b$ where $a, b \in \mathbb{Z}$ . Find the value of $a+b$ .
Total Mark	2
Correct Answer	6
Explanation	n/a
Mark Scheme	$g \circ f(x)=g(f(x))=2 \sin \left(3 x+\frac{\pi}{4}\right)+3$ Since $-1 \leq \sin \theta \leq+1$ the range is, $1 \leq g \circ f(x) \leq 5$ $$ Thus, $a+b=6$ .
Question Text	(b) Select the solution to $g∘f(x)=5$ . (A) $\frac{3 \pi}{12}$ (B) $\frac{11 \pi}{12}$ (C) $\frac{17 \pi}{12}$ (D) $\frac{25 \pi}{12}$
Total Mark	2
Correct Answer	(d)
Explanation	n/a
Mark Scheme	$2 \sin \left(3 x+\frac{\pi}{4}\right)+3=5 \\ \sin \left(3 x+\frac{\pi}{4}\right)=1 \\ x=\frac{\pi}{12}+2 n \pi$
Question Text	(c) The graph of $y=g \circ f(x)$ can be obtained by applying four transformations to the graph of $y=\sin x$ as listed below Stretch scale factor $a$ parallel to $y$ -axis (vertically). Vertical translation of $b$ units up Stretch scale factor $\frac{1}{c}$ parallel to $x$ axis (horizontally) Horizontal translation of $\frac{\pi}{d}$ to the left. Given that $a, b, c, d \in \mathbb{Z}$ , compute $a+b+c+d$
Total Mark	3
Correct Answer	12
Explanation	n/a
Mark Scheme	From (a), $g \circ f(x)=g(f(x))=2 \sin \left(3 x+\frac{\pi}{4}\right)+3$ Thus, $2+3+3+4=12$

Topic	2.3 Transformation
Tag	Transformation; Functions; Domain Range; Asymptotes; Graph; Reflection; Scale factor; Translation; Stretch;
Source	M15-TZ2-P1-10(HL)
Question Text	(a) Sketch the graph of $y=f(x)$ , indicating clearly any asymptotes and points of intersection with the $x$ and $y$ axes.

Total Mark	4
Correct Answer	(a)
Explanation	n/a
Mark Scheme	x-intercept at $(0, 0)$ , $f(x) > 0$ , when $x > 1$
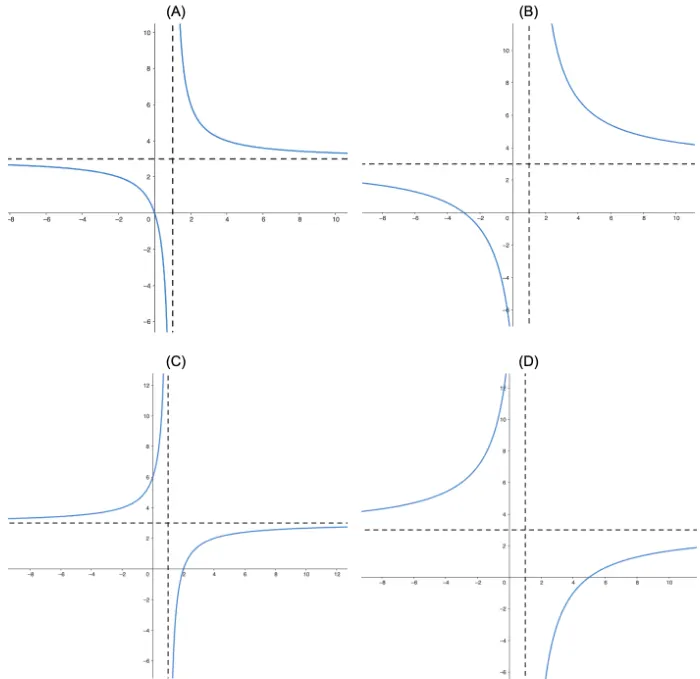
Question Text	(b) Find an expression for $f^{-1}(x)$ . (A) $f^{-1}(x)=\frac{x}{x-3}$ (B) $f^{-1}(x)=\frac{x-1}{3 x}$ (C) $f^{-1}(x)=\frac{x-1}{3 x}$ (D) $f^{-1}(x)=\frac{x}{3 x-1}$
Total Mark	4
Correct Answer	(a)
Explanation	n/a
Mark Scheme	Take the inverse of $f(x)=\frac{3 x}{x-1}$ $x=\frac{3 y}{y-1} \\ x(y-1)=3 y \\ y(x-3)=x \\ y=\frac{x}{x-3}$
Question Text	(c) Find the sum of the values of $x$ for which $f(x)=f^{-1}(x)$ .
Total Mark	3
Correct Answer	4
Explanation	n/a
Mark Scheme	$\frac{x}{x-3}=\frac{3 x}{x-1} \\ x(x-1)=3 x(x-3) \\ x(2 x-8)=0 \\ x=0 \text { or } 4$
Question Text	The solution to the inequality $\|f(x)\| < 2$ can be written as $a < x < b/c$ where $a$ is an integer and $b,$ $c$ are positive integers in lowest terms. Compute the value of $b + c - a$ . [4] 4
Total Mark	4
Correct Answer	0
Explanation	n/a
Mark Scheme	n/a

Topic	2.3 Transformation
Tag	Transformation; Functions; Domain Range; Asymptotes; Graph; Reflection; Scale factor; Translation; Stretch;
Source	N14/5/MATHL/HP1/ENG/TZ0/XX/1
Question Text	The function $f$ is defined by $f(x)=\frac{1}{x}, x \neq 0.$ The graph of the function $y=g(x)$ is obtained by applying the following transformation to the graph of $y=f(x):$ A horizontal translation of 3 units to the right; A vertical translation of 2 units up (a) Which is the correct expression for $g(x)$ ? (A) $g(x)=\frac{1}{x-2}+3$ (B) $g(x)=\frac{1}{x+2}+3$ (C) $g(x)=\frac{1}{x-3}+2$ (D) $g(x)=\frac{1}{x+3}+2$
Total Mark	3
Correct Answer	(b)
Explanation	n/a
Mark Scheme	$g(x)=\frac{1}{x-3}+2$
Question Text	(b) The two asymptotes of $g(x)$ can be written as $x = a$ and $y = b$ where $a, b ∈ ℤ+$ . Find $a + b$ .
Total Mark	2
Correct Answer	5
Explanation	n/a
Mark Scheme	$x=3$ , $y=2$ Thus, $a + b = 5$

Topic	2.3 Transformation
Tag	Transformation; Functions; Domain Range; Asymptotes; Graph; Reflection; Scale factor; Translation; Stretch;
Source	M13-TZ2-P1-12(HL)
Question Text	The function $f$ is defined by $f(x)=\frac{2 x-3}{x+2}$ , with domain $D=\{x:-3 \leq x \leq 5\}$ . (a) Express $f(x)$ in the form $A+\frac{B}{x+2}$ , where $A$ and $B \in Z$ . Find the sum of $A$ and $B$ .
Total Mark	2
Correct Answer	-5
Explanation	n/a
Mark Scheme	$f(x)=\frac{2 x-3}{x+2}=\frac{2 x+4-7}{x+2}=2-\frac{7}{x+2}$ Hence, the sum of $A$ and $B$ is $2-7=-5$ .
Question Text	(b) The range of $f$ can be expressed as $p, q$ . Find the sum of $p$ and $q$ .
Total Mark	2
Correct Answer	10
Explanation	n/a
Mark Scheme	Considering the domain of function $f$ , we can calculate the range of $f$ . $f(-3)=9$ $f(5)=1$ Since, $p=1$ and $q=9$ , the sum of $p$ and $q$ is equal to 10.
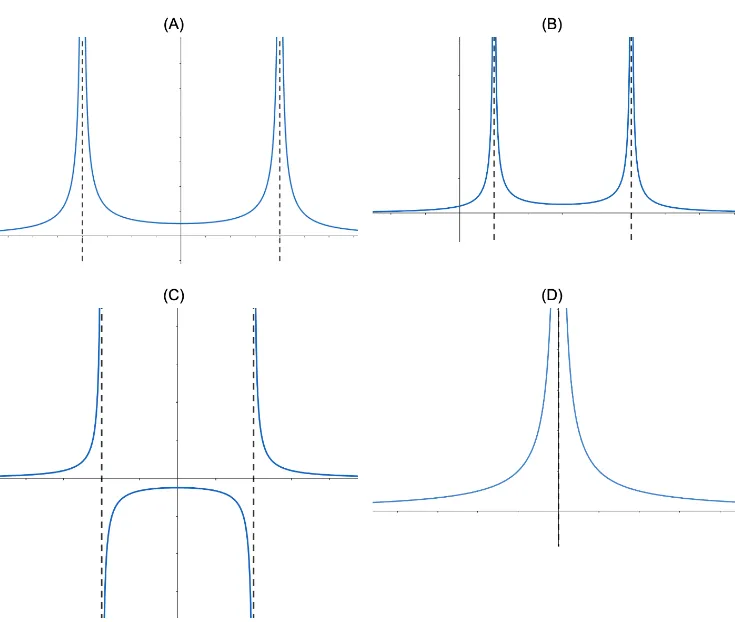
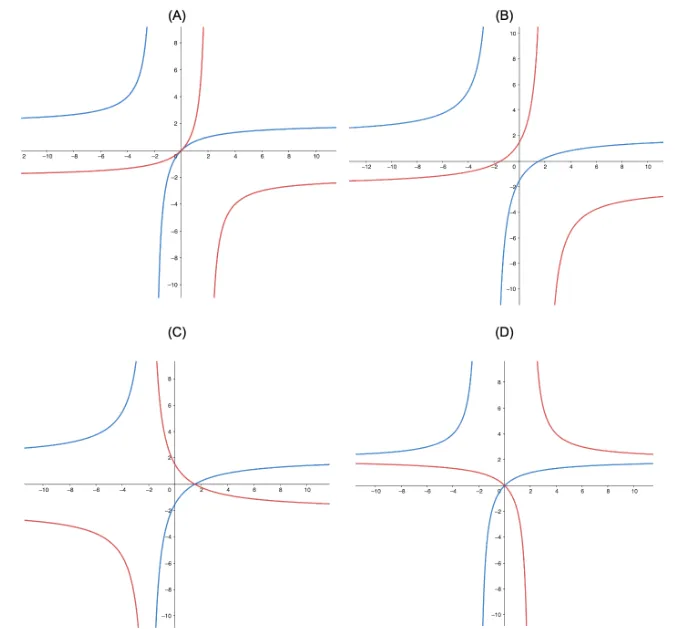
Question Text	(c) (i) Find an expression for $f^{-1}(x)$ . (A) $f^{-1}(x)=\frac{2 x+3}{2-x}$ (B) $f^{-1}(x)=\frac{2 x-3}{2+x}$ (C) $f^{-1}(x)=\frac{x+3}{2-2 x}$ (D) $f^{-1}(x)=\frac{x-3}{2+2 x}$ Total Mark: (a) Correct Answer: 3 Explanation: n/a Mark Scheme: Take the inverse, $x=\frac{2 y-3}{y+2} \\ x(y+2)=2 y-3 \\ y(2-x)=2 x+3 \\ y=\frac{2 x+3}{2-x}$ (ii) Select the option that accurately plots the graph of $y=f(x)$ , and the graph of $y=f^{-1}(x)$ .

Question Text	Total Mark: 8 Correct Answer: (b) Explanation: n/a Mark Scheme: $x$ -intercept is non zero. The functions are mirror images across the line $y=x$
Question Text	(d) (i) On a different diagram, sketch the graph of $y=f(\|x\|)$ where $x \in D$ .

Question Text

Total Mark: (d) Correct Answer: 3 Explanation: n/a Mark Scheme: To draw the graph, apply the absolute value of

x

and calculate the

y

coordinate accordingly. (ii) Select all solutions of the equation

f(|x|)=1

. (A) 10 (B) -7 (C) 7 (D) 5 (E) -5 Total Mark: 4 Correct Answer: 5, -5 Explanation: n/a Mark Scheme: Attempt to solve

f(|x|)=1

.

2-\frac{7}{|x|+2}=1 \\ |x|=5 \\ x=-5 \text { or } 5

Topic	2.3 Transformation
Tag	Transformation; Functions; Domain Range; Asymptotes; Graph; Reflection; Scale factor; Translation; Stretch;
Source	M19/5/MATHL/HP1/ENG/TZ1/XX/10 c
Question Text	The function px is defined by $p(x) = x³ - 2x² + 7x + 17$ where $x ∈ R$ . Write down the transformation that will transform the graph of $y = p(x)$ onto the graph of $y = 64x³ - 32x² + 28x - 17$ . (A) Translate four units to the left (B) Translate four units to the right (C) Stretch parallel to the x-axis, scale factor 0.25 (D) Stretch parallel to the x-axis, scale factor 4
Total Mark	3
Correct Answer	(d)
Explanation	n/a
Mark Scheme	For this question, we need to find the transformation that will transform $p(x)$ to $y$ . When we stretch $p(x)$ parallel to the $x -$ axis by the scale factor of 0.25 , $y=p(4 x) \\ y=(4 x)^3-2(4 x)^2+7(4 x)+17 \\ y=64 x^3-32 x^2+28 x+17$ Hence, the answer is option C.

Topic	2.3 Transformation
Tag	Transformation; Functions; Domain Range; Asymptotes; Graph; Reflection; Scale factor; Translation; Stretch;
Source	M19/5/MATHL/HP1/ENG/TZ2/XX/3
Question Text	Consider the function $f(x)=x⁴ - 3x² - 4x + 8,x∈R$ . The graph of is translated three units to the right to form the function $g(x)$ . Express $g(x)$ in the form $ax⁴ + bx³ + cx² + dx+e$ where $a, b, c, d, e ∈ Z$ and find the sum of $a, b, c, d,$ and $e$ .
Total Mark	5
Correct Answer	47
Explanation	n/a
Mark Scheme	Since $g(x)$ is formed when $f(x)$ is translated three units to the right, we can express $g(x)$ in terms of $f(x)$ like the following, $g(x)=f(x-3) \\ g(x)=(x-3)^4-3(x-3)^2-4(x-3)+8 \\ g(x)=(x-3)^4-3(x-3)^2-4(x-3)+8$ First, attempt to expand $(x-3)^4$ $(x-3)^4 =x^4-4\left(3 x^3\right)+6\left(3^2 x^2\right)-4\left(3^3 x\right)+3^4 \\=x^4-12 x^3+54 x^2-108 x+81$ Next, substitute the expression into $g(x)$ $g(x)=x^4-12 x^3+54 x^2-108 x+81-3\left(x^2-6 x+9\right)-4 x+12+8 \\ =x^4-12 x^3+51 x^2-94 x+101$ Hence, the sum of all the coefficients is equal to $1-12+51-94+101=47$

Topic	2.3 Transformation
Tag	Transformation; Functions; Domain Range; Asymptotes; Graph; Reflection; Scale factor; Translation; Stretch;
Source	M19/5/MATHL/HP1/ENG/TZ2/XX/11
Question Text	Consider the functions $f$ and $g$ defined by $f(x)=\ln \|x\|, x \in R \backslash\{x \neq 0\}$ and $g(x)=\ln \|x-k\|$ , $x \in R \backslash\{x \neq k\}$ , where $k \in R, k>3$ . (a) State the range of $g$ . (A) $g(x) \in R, g(x)<0$ (B) $g(x) \in R, g(x)>2$ (C) $g(x) \in R, g(x)<2$ (D) $g(x) \in R$
Total Mark	1
Correct Answer	(d)
Explanation	n/a
Mark Scheme	The range of $g(x)$ includes all real numbers.
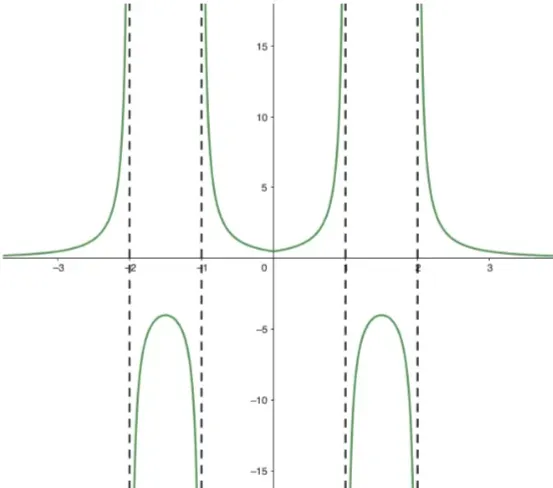
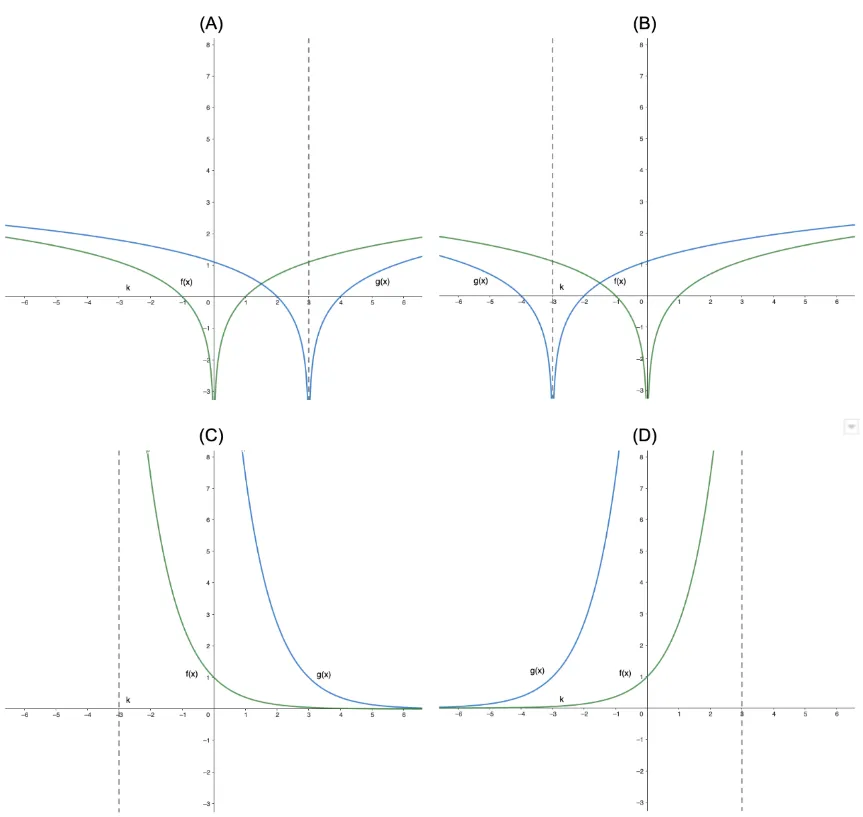
Question Text	(b) Sketch the graphs of $y=f(x)$ and $y=g(x)$ on the same axes, clearly stating the points of intersection with any axes.

Total Mark	6
Correct Answer	(a)
Explanation	n/a
Mark Scheme	The vertical asymptote of $g(x)$ is located at $x=3$ since the domain of $g(x)$ includes all real numbers except 3. In addition, the $x$ -intercept of $g(x)$ is located at $x=2$ and $x=4$ and the $x$ -intercept of $f(x)$ is located at $x=-1$ and $x=1$ . Hence, the correct graph of $f(x)$ and $g(x)$ is presented in A.
Question Text	The graphs of $f$ and $g$ intersect at the point $P$ . (c) Find the coordinates of $P$ . (A) $P\left(\frac{k}{2},-\ln \frac{k}{2}\right)$ (B) $P\left(-\frac{k}{2}, \ln \frac{k}{2}\right)$ (C) $P\left(\frac{k}{2}, \ln \frac{k}{2}\right)$ (D) $P(-k, \ln k)$
Total Mark	2
Correct Answer	(c)
Explanation	n/a
Mark Scheme	Since point $P$ is the intersection of graph $f$ and $g$ , the $x$ -coordinate can be found by $\ln (-x+k)=\ln (x) \\ -x+k=x \\ x=\frac{k}{2}, y=\ln \left(\frac{k}{2}\right)$

2.3 Transformation

Q1

Q2

Q3

Q4

Q5

Q6

Q7

Q8

Q9

Q10