home
Mission
//////
home
//////

A.3 Work, Energy and Power

생성일
2024/07/05 08:03
태그

A.3.1 Work

Work
•
Energy exists in many forms, but most commonly if it is stored energy it is called potential energy and when the energy is in motion of an object it is called kinetic energy.
•
An object at rest can be assumed to have zero kinetic energy, and an object in motion will have kinetic energy higher than zero.
•
Objects that move faster have more kinetic energy.
•
Since forces cause objects to move faster or slower, forces are what causes the energy to increase or decrease.
•
Energy transferred to or from an object via the application of force along a displacement is referred to as work.
•
Since work refers to the energy transferred to or from the object it is also defined as the change in energy
•
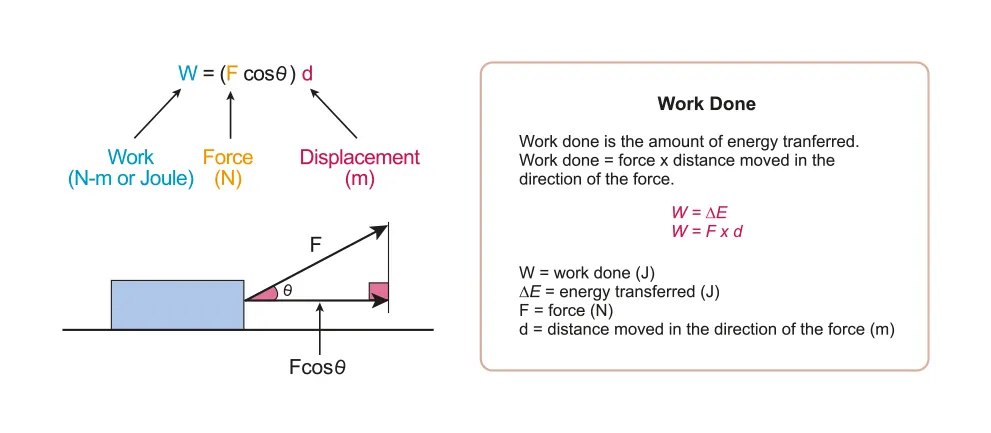
Work is formally defined as the product of the force and displacement in the same direction as the force.
W=F⋅s⋅cosθ W=F\cdot s \cdot cos\theta 
•
Thus a force will only do work if there is a displacement in the same direction as the force
•
If the angle between the force and the displacement is 90 degrees work done is zero
•
A force does negative work if it has a component in the opposite direction as the displacement (angle
•
between 90° and 180°)
•
A force does positive work if it has a component in the same direction as the displacement (angle between 0° and 90°)
•
Work is also the area under the force-displacement graph
A.3.1-1 Work done by the force F

A.3.2 Energy

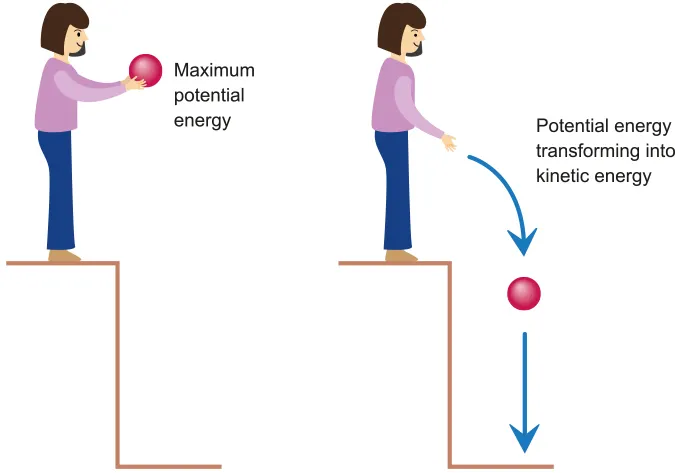
Gravitational Potential Energy (GPE)
•
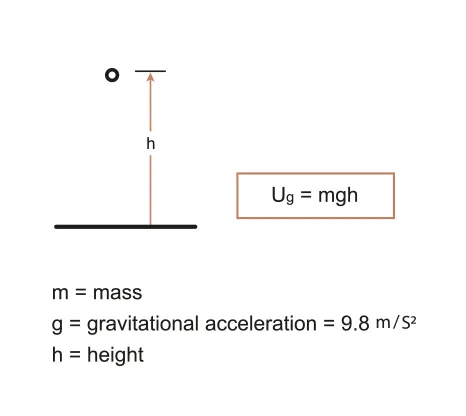
GPE is energy stored in a mass due to its position in the gravitational field
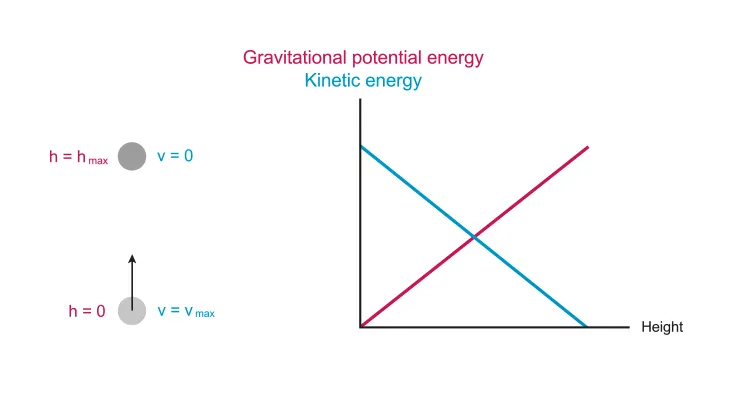
A.3.2-1 Diagram and graph showing the transition of energy
•
If the mass is lifted, it will gain potential energy (Converted from another energy)
•
If the mass falls, it will lose potential energy (Converted to another energy)
•
In a uniform gravitational field, the formula for gravitational potential energy is:
W=ΔE=pmgΔhW=\Delta E=_{p}mg\Delta h
A.3.2-2 Diagram explaining Gravitational Potential energy with equation
Work in a Spring System
•
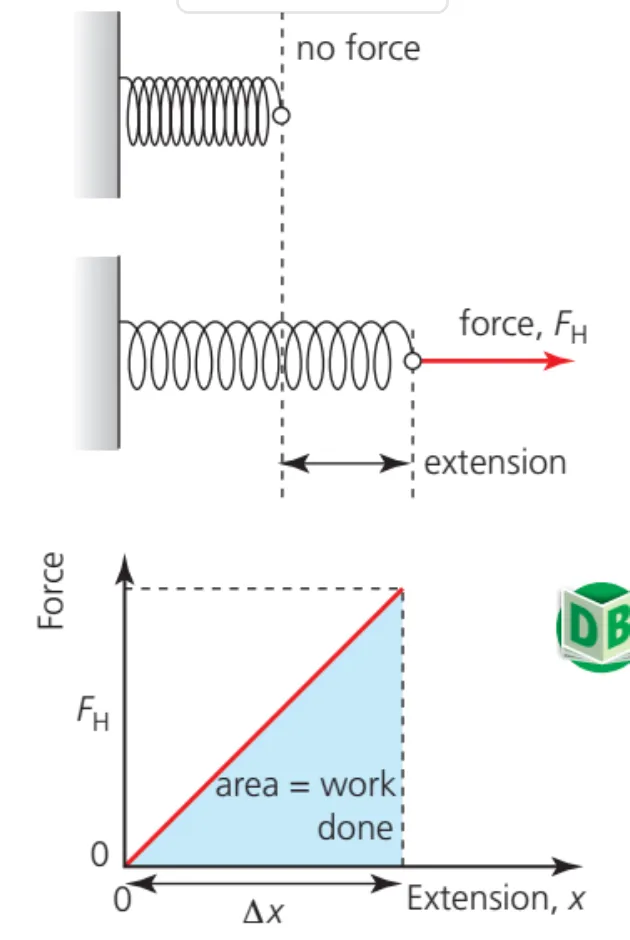
In a spring system, the spring force is determined by the multiplication of the spring coefficient and how much distance the spring gets compressed
◦
Mathematically:
F=−kxF = -kx
•
Therefore, the work done in compressing or extending a spring could be calculated by using integral calculus
W=−12kx2W=-\frac{1}{2}kx^{2}
Kinetic Energy (Ek)(E_{k})
•
Kinetic energy is the energy that it possesses due to the object’s motion
•
the work needed to accelerate a body of a given mass from rest to its stated velocity
◦
For a non-rotating body, the kinetic energy is 12mv2 \frac{1}{2}mv^{2}
◦
The SI unit of kinetic energy is Joule
A.3.2-3 Exampler Diagram of GPE to KE conversion
Work-Energy Principle
•
In a perfectly ideal situation, the system’s energy will be conserved, whi ch is called conservation of energy
•
Under such a situation, a system usually only contains mechanical energy which is the summation of kinetic energy and potential energy
◦
Therefore, there will be energy conversion between these two kinds of energy.
•
Mathematically :
∑W=ΔEk\sum W=\Delta E_{k}
•
General derivation :
∑W=∫dw=∫12d(22)=12m(v22−v12)=ΔEk\sum W=\int dw=\int_{1}^{2}d(\frac{}{2}^{2})=\frac{1}{2}m(v{_{2}}^{2}-v{_{1}}^{2})=\Delta E_{k}
•
When thinking about ∑W\sum W, students should summate all the work done in the system

A.3.3 Power and Efficiency

Power
•
Power is defined as the rate at which energy is transferred
◦
This is the same as the rate at which work is done :
P=wt=energy transferredtime takenP = \frac{w}{t}=\frac{energy\ transferred}{time\ taken}
◦
Unit of power is Watt (W)
◦
SI units is J/s
•
If the object is moving at constant velocity against a constant force, the power needed is P=Fv
Efficiency
•
Depending on the situation, we can categorize the energy transferred as useful or not
•
Efficiency is an important measure to decide such tendencies
•
We define efficiency as a ratio of useful energy to the total energy transferred
◦
Mathematically:
η=useful work OUTtotal work IN=useful energy OUTtotal energy IN=useful power OUTtotal power IN\eta =\frac{useful~work~OUT}{total~work~IN}=\frac{useful~energy~OUT}{total~energy~IN}=\frac{useful~power~OUT}{total~power~IN}

A.3.4 Energy Density

Energy density
•
Energy density is defined as the energy available per unit volume of a fuel
•
energy density=total energy availablevolumeenergy~density = \frac{total~energy\ available}{volume}