home
Mission
///////
home
///////

5.3 Application of Differential Calculus

Q1

Topic
5.3 Application of Differential Calculus
Tag
Differentiation Tangent Optimization Related Rates Kinematics Euler's Method Maclaurin Series Trigonometric Functions Logarithmic Functions Modelling
Source
N14/5/MATHL/HP1/ENG/TZ0/XX/5
Question Text
A tranquilizer is injected into a muscle from which it enters the bloodstream. The concentration CC in mgll−1^{-1}, of tranquilizer. In the bloodstream can be modeled by the function C(t)=5t4+t2,t≥0C(t)=\frac{5 t}{4+\mathrm{t}^2}, t \geq 0 where tt is the number of minutes after the injection. The maximum concentration of tranquilizer in the bloodstream can be expressed as nm\frac{n}{m} in its simplest form. Find the sum of nn and mm.
Total Mark
6
Correct Answer
9
Explanation
n/a
Mark Scheme
Use of the quotient rule C′(t)=(4+t2)×5−5t×2t(4+t2)2=20−5t2(4+t2)2C^{\prime}(t)=\frac{\left(4+t^2\right) \times 5-5 t \times 2 t}{\left(4+t^2\right)^2}=\frac{20-5 t^2}{\left(4+t^2\right)^2} At the local maximum, the first derivative should be equal to 0 . C′(t)=0t=2 (minutes) C^{\prime}(t)=0 \\ t=2 \text { (minutes) } In this real-life application, the value of tt cannot be a negative value as it represents the number of minutes. To find the maximum concentration, substitute the tt value into the original function. C(2)=54(mgl−1)C(2)=\frac{5}{4}\left(\mathrm{mgl}^{-1}\right) Hence, m+n=4+5=9m+n=4+5=9.

Q2

Topic
5.3 Application of Differential Calculus
Tag
Differentiation Tangent Optimization Related Rates Kinematics Euler's Method Maclaurin Series Trigonometric Functions Logarithmic Functions Modelling
Source
M14/5/MATHL/HP1/ENG/TZ1/X/8
Question Text
A box is moving in a straight line. When it is s meters from a fixed point PP on the line its velocity, vv, is given by v=−1s3,s>0v=-\frac{1}{s^3}, s>0. Find the acceleration of the box when it is 80 cm from PP to the nearest ms−2^{-2}.
Total Mark
6
Correct Answer
-14
Explanation
n/a
Mark Scheme
The acceleration of the box is calculated as below dvds=3s−4a=vdvds=−1s3×3s4=−3s7\frac{d v}{d s}=3 s^{-4} \\ a=v \frac{d v}{d s}=-\frac{1}{s^3} \times \frac{3}{s^4}=-\frac{3}{s^7} Since ss is expressed in meters, 80 cm is equal to s=45s=\frac{4}{5}. We can substitute this value into the acceleration formula. When s=13,a=−3(45)7=−14.305≈−14 ms−2s=\frac{1}{3}, a=-\frac{3}{\left(\frac{4}{5}\right)^7}=-14.305 \approx-14 \mathrm{~ms}^{-2}

Q3

Topic
5.3 Application of Differential Calculus
Tag
Differentiation Tangent Optimization Related Rates Kinematics Euler's Method Maclaurin Series Trigonometric Functions Logarithmic Functions Modelling
Source
M13-TZ1-P1-5(HL)
Question Text
Paint is poured into a tray where it forms a circular pool with a uniform thickness of 0.5 cm. If the paint is poured at a constant rate of 4 cm3^3s−1^{-1}, the rate of increase of the radius of the circle when the radius is 40 cm can be expressed as 1xπ\frac{1}{x\pi} in its simplest form. Find the value of xx.
Total Mark
6
Correct Answer
10
Explanation
n/a
Mark Scheme
The volume of a circle is equal to V=0.5πr2V=0.5 \pi r^2 Using the given volume's rate of change, we can derive the following expression. dVdr=πr⋅dVdt=4\frac{d V}{d r}=\pi r \cdot \frac{d V}{d t}=4 Applying the chain rule, we can calculate the rate of change of the circle's radius. drdt=dVdt×drdVdrdt=4×1πr\frac{d r}{d t}=\frac{d V}{d t} \times \frac{d r}{d V} \\ \frac{d r}{d t}=4 \times \frac{1}{\pi r} When the radius is 40 cm , drdt=440π=110π\frac{d r}{d t}=\frac{4}{40 \pi}=\frac{1}{10 \pi} Hence, x=10x=10.

Q4

Topic
5.3 Application of Differential Calculus
Tag
Differentiation, Quotient rule
Source
N19/5/MATHL/HP1/ENG/TZ1/XX/10
Question Text
Consider f(x)=3x−6x2−1,−1<x<1f(x)=\frac{3 x-6}{x^2-1},-1<x<1 (a) (i) Find f′(x)f^{\prime}(x). (a) 3x2+4x−1(x2−1)2\frac{3 x^2+4 x-1}{\left(x^2-1\right)^2} (b) x2−4x−1(x2−1)2\frac{x^2-4 x-1}{\left(x^2-1\right)^2} (c) x2−4x+1(x2−1)2\frac{x^2-4 x+1}{\left(x^2-1\right)^2} (d) −x2−4x+1(x2−1)2\frac{-x^2-4 x+1}{\left(x^2-1\right)^2} Total Mark: 3 Correct Answer: c Explanation: n/a Mark Scheme: Attempt to use the quotient rule (or equivalent) f′(x)=(x2−1)(3)−(3x−6)(2x)(x2−1)2=−3x2+12x−3(x2−1)2=x2−4x+1(x2−1)2f^{\prime}(x)=\frac{\left(x^2-1\right)(3)-(3 x-6)(2 x)}{\left(x^2-1\right)^2} \\ =\frac{-3 x^2+12 x-3}{\left(x^2-1\right)^2}=\frac{x^2-4 x+1}{\left(x^2-1\right)^2} (ii) Find the value of f′(x)f^{\prime}(x) when x=2−3x=2-\sqrt{3} Total Mark: 2 Correct Answer: 0 Explanation: n/a Mark Scheme: Substitute 2−32-\sqrt{3} into f′(x)f^{\prime}(x) from (a)(i). f′(x)=0f^{\prime}(x)=0
Question Text
(b) For the graph of y=f(x)y=f(x), (i) The yy-intercept is (0,b)(0, b). Find the value of bb. Total Mark : 2 Correct Answer : 6 Explanation : na Mark Scheme : The yy-intercept is located at (0,6)(0,6). Therefore, the value of bb is 6 . Answer: 6 (ii) The horizontal asymptote of f(x)f(x) is located at y=ay=a. Find the value(s) of aa. Total Mark : 3 Correct Answer : 0 Explanation : na Mark Scheme : Since the degree of the denominator is greater than the degree of the numerator, the horizontal asymptote is the xx-axis. Hence, the value of aa is 0 . Answer: 0

Q5

Topic
5.3 Application of Differential Calculus
Tag
Source
M19/5/MATHL/HP1/ENG/TZ2/XX/8 a,b
Question Text
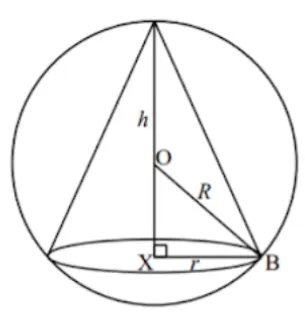
A right circular cone of radius rr is inscribed in a sphere with centre OO and radius RR as shown in the following diagram. The perpendicular height of the cone is h,Xh, X denotes the centre of its base and B a point where the cone touches the sphere. (a) The volume of the cone may be expressed by V=π3(aRh2−h3)V=\frac{\pi}{3}\left(a R h^2-h^3\right). Find the value of aa.
Total Mark
4
Correct Answer
2
Explanation
n/a
Mark Scheme
Attempt to use Pythagoras theorem in the triangle OXBO X B. r2=R2−(h−R)2r^2=R^2-(h-R)^2 Substitute the expression for r2r^2 into formula for volume of cone V=πr2h3V=\frac{\pi r^2 h}{3}. V=πh3(R2−(h−R)2)V=πh3(R2−(h2+R2−2hR))V=πh3(2hR−h2)V=π3(2Rh2−h3)\begin{gathered} V=\frac{\pi h}{3}\left(R^2-(h-R)^2\right) \\ V=\frac{\pi h}{3}\left(R^2-\left(h^2+R^2-2 h R\right)\right) \\ V=\frac{\pi h}{3}\left(2 h R-h^2\right) \\ V=\frac{\pi}{3}\left(2 R h^2-h^3\right) \end{gathered} Hence, a=2a=2. Answer: 2
Question Text
(b) Given that there is one inscribed cone having a maximum volume, show that the volume of this cone is 32πR3G\frac{32 \pi R^3}{G}. Find the value of GG.
Total Mark
4
Correct Answer
81
Explanation
n/a
Mark Scheme
When the cone reaches its maximum volume, the volume's rate of change is equal to 0:dVdh=00: \frac{d V}{d h}=0. We can express the height of the cone in terms of RR by using the first derivative of the volume expression. dVdh=π3(4Rh−3h2)4Rh=3h2h=4R3( since h≠0) \begin{gathered} \frac{d V}{d h}=\frac{\pi}{3}\left(4 R h-3 h^2\right) \\ 4 R h=3 h^2 \\ h=\frac{4 R}{3}(\text { since } h \neq 0) \end{gathered} Now, we can express the cone's volume in terms of RR to find the value of GG. Vmax⁡=π3(2R(4R3)2−(4R3)3)Vmax⁡=π3(2R16R29−(64R327))Vmax⁡=32πR381\begin{gathered} V_{\max }=\frac{\pi}{3}\left(2 R\left(\frac{4 R}{3}\right)^2-\left(\frac{4 R}{3}\right)^3\right) \\ V_{\max }=\frac{\pi}{3}\left(2 R \frac{16 R^2}{9}-\left(\frac{64 R^3}{27}\right)\right) \\ V_{\max }=\frac{32 \pi R^3}{81} \end{gathered} Hence, G=81G=81. Answer: 81

Q6

Topic
5.3 Application of Differential Calculus
Tag
Differentiation, Quotient rule
Source
M18/5/MATHL/HP1/ENG/TZ2/XX/4
Question Text
Consider the curve y=11−x+4x−4y=\frac{1}{1-x}+\frac{4}{x-4}. Find the xx-coordinates of the points on the curve when the gradient is zero. (a) 0 (b) 1 (c) -1 (d) 2 (e) -2
Total Mark
6
Correct Answer
d,e
Explanation
n/a
Mark Scheme
Combine the fractions: y=11−x+4x−4=−3x−x2+5x−4y = \frac{1}{1 - x} + \frac{4}{x - 4} = \frac{-3x}{−x^2+5x−4} Differentiate yy to find dydx\frac{dy}{dx}: dydx=−3(−x2+5x−4)+3x(−2x+5)[−x2+5x−4]2=−3(x2−4)[−x2+5x−4]2\frac{dy}{dx} = \frac{-3(−x^2+5x−4) + 3x(-2x+5)}{[−x^2+5x−4]^2}= \frac{-3(x^2-4)}{[−x^2+5x−4]^2} When dydx=0\frac{dy}{dx}=0, x=2,−2x=2,-2