C.4.1 The nature of standing waves
Standing waves result from the superposition of two opposite identical waves:
Standing waves are formed when the two waves interfere with:
•
the same amplitude
•
the same frequency
•
traveling in opposite directions
In standing waves:
•
the positions of the crests and troughs do not change
•
energy is not transferred yet there is energy associated with it.
•
Nodes: the points where the total displacement always remains zero
•
Antinodes: the points where the displacement varies between a maximum in one direction and in the other direction
C.4.1-1 A standing wave - the pattern remains fixed
Stationary Wave | Normal (Travelling) Wave | |
Amplitude | All points on the wave have different amplitudes. The maximum amplitude is 2A at the antinodes. It is zero at the nodes. | All points on the wave have the same amplitude. |
Frequency | All points oscillate with the same frequency. | All points oscillate with the same frequency. |
Wavelength | This is twice the distance from one node (or antinode) to the next node (or antinode). | This is the shortest distance (in metres) along the wave between two points that are in phase with one another. |
Phase | All points between one node and the next node are moving in phase. | All points along a wavelength have different phases. |
Energy | Energy is not transmitted by the wave, but it does have an energy associated with it. | Energy is transmitted by the wave. |
C.4.2 Boundary conditions
Transverse waves on a string
•
If the string is fixed at the ends, the corresponding part of the string cannot oscillate.
•
Here, both ends of the string reflect the traveling wave and thus creates a standing wave.
•
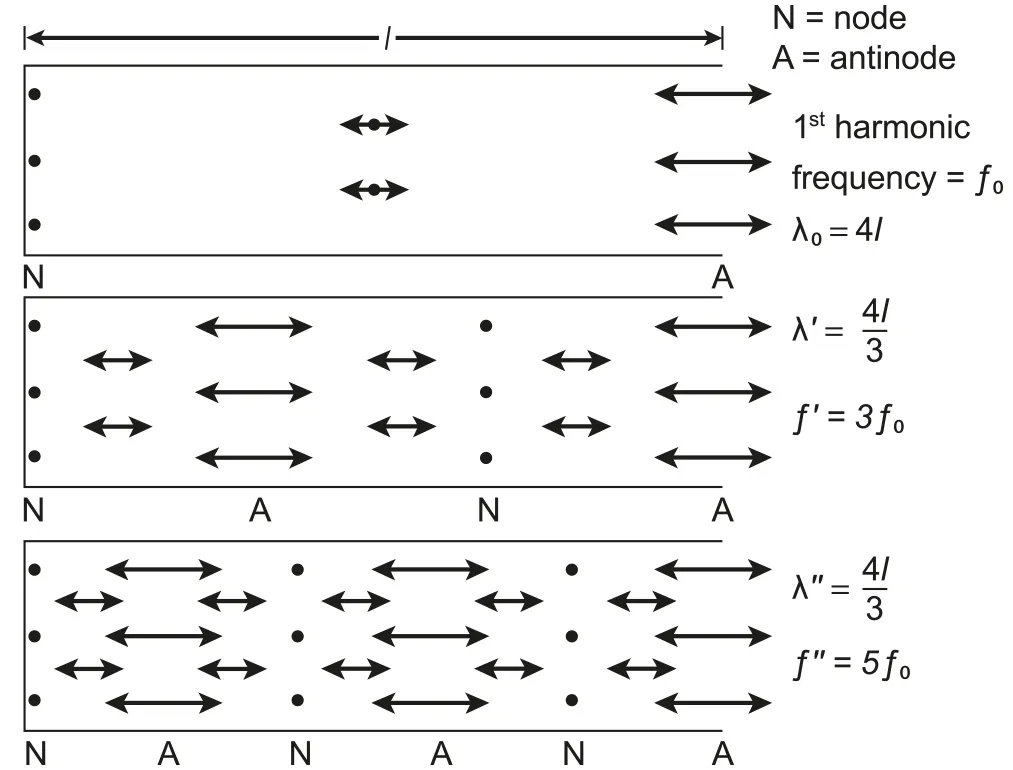
The diagram below demonstrates the possible resonant modes.
C.4.2-1 Harmonics with notations
•
The first (fundamental) harmonic: the resonant mode that has the lowest frequency
◦
The frequency at which the string vibrates with a large amplitude in the form of a single loop
•
Higher resonant modes are called harmonics
Longitudinal and sound waves in a pipe
•
Likewise transverse waves on a string, the boundary conditions determine the standing waves that can possibly exist in the tubes.
•
closed ends → displacement nodes, open ends → antinodes
•
Harmonic modes for a pipe open at both ends
C.4.2-2 harmonics in both open ends pipe with notations
•
Harmonic modes for a pipe closed at one end
C.4.2-3 harmonics in one open end pipe with notations
Behavior of standing waves in pipes and strings:
1.
One closed end and one open end (pipes)
2. Two closed ends (strings)
3.
Two open ends (pipe)
For standing waves, (the distance between adjacent nodes) = (the distance between adjacent antinodes) =.
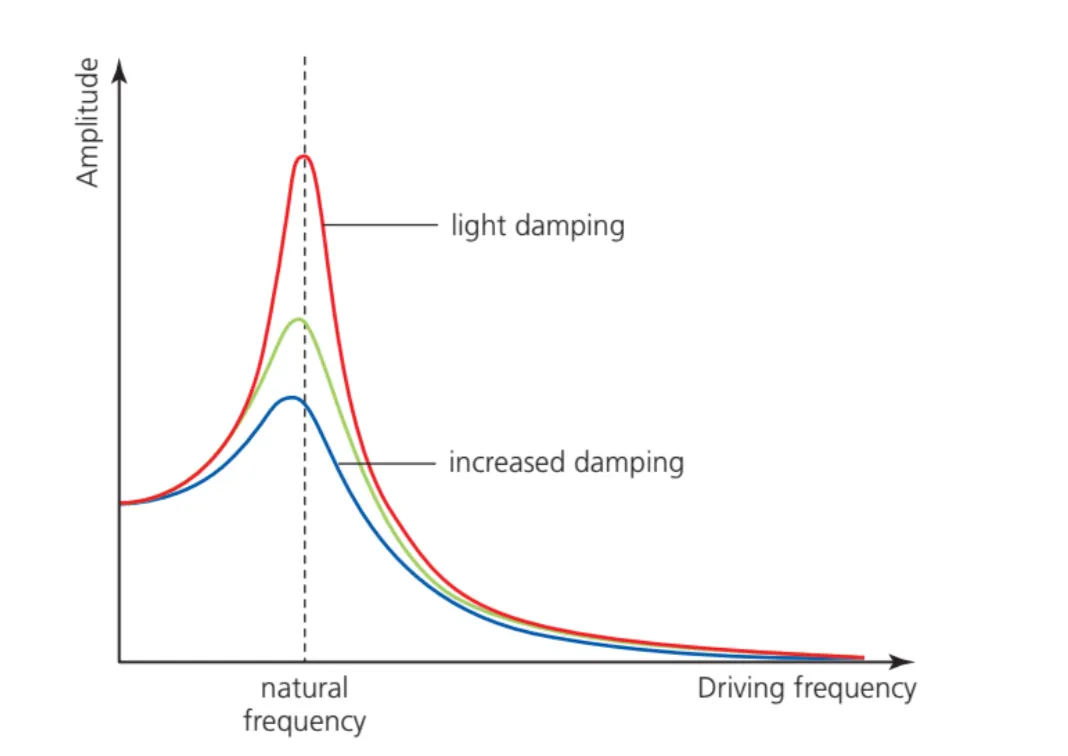
C.4.3 Resonance
Natural Frequency
Driving Frequency
Amplitude of Oscillation
C.4.3-1
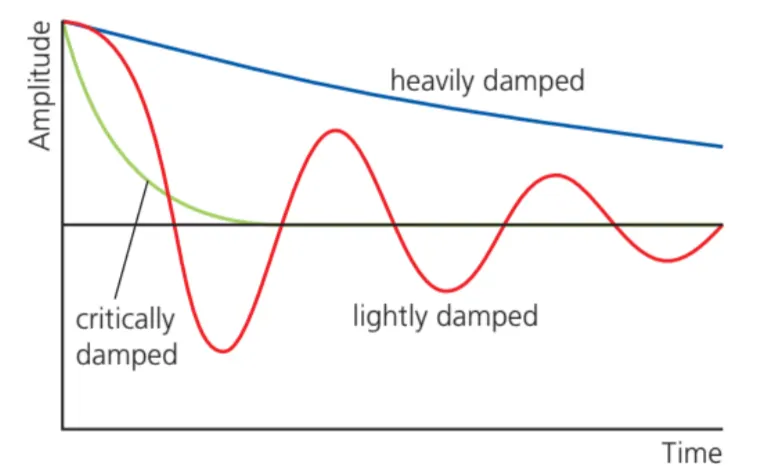
C.4.4 Damping
Effect on Maximum Amplitude
Effect on Resonant Frequency
Types of Damping
C.4.4-1