2.1 Functions

Topic	2.1 Functions
Tag	Domain; Range; Functions; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source	N17/5/MATHL/HP1/ENG/TZ0/XX/6
Question Text	(a) Sketch the graph of $y=\frac{1-3 x}{x-3}$ , showing clearly any asymptotes and stating the coordinates of any points of intersection with the axes.

Total Mark	4
Correct Answer	a
Explanation	na
Mark Scheme	Vertical asymptote : $x$ =3 $y=\frac{1-3 x}{x-3}=-3-\frac{8}{x-3}$ Horizontal asymbotote: $y$ =-3 $y=\frac{1-3 \times 0}{0-3}=\frac{-2}{-3}=\frac{2}{3}$ $y$ -intercept: $\left(0, \frac{2}{3}\right)$ Answer: a
Question Text	(b) The solution to the inequality $\left\|\frac{1-3 x}{x-3}\right\|$ <2, can be written as $a$ < $x$ < $\frac{b}{c}$ , where $a, b, c$ $\in$ $Z$ . Find the value of $a+b+c$ .
Total Mark	5
Correct Answer	7
Explanation	na
Mark Scheme	Consider the visual interpretation of the graph,

\begin{gathered} \frac{1-3 x}{x-3}=2, x=\frac{7}{5} \\ -\left(\frac{1-3 x}{x-3}\right)=2, x=-5 \end{gathered}

Thus,

\begin{gathered} -5<x<\frac{7}{5} \\ a+b+c=-5+7+5=7 \end{gathered}

Answer: 7

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source	N17/5/MATHL/HP1/ENG/TZ0/XX/11a
Question Text	Consider the function $f_n(x)=2^n(\sin 2 x)(\cos 2 x)(\cos 4 x) \ldots\left(\cos 2^n x\right), n \in Z^{+}$ . Determine whether $f_n$ is an odd or even function.
Total Mark	4
Correct Answer	odd
Explanation	na
Mark Scheme	Applying the sine double angle identity, a pattern can be noticed $f_n(x)=2^n(\sin 2 x)(\cos 2 x)(\cos 4 x) \ldots\left(\cos 2^n x\right)=2\left(\sin \left(2^n x\right)\right)$ Since $\sin (\theta)=-\sin (-\theta)$ , It is an odd function.

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source	M17/5/MATHL/HP1/ENG/TZ1/XX
Question Text	Consider the function $f(x)=\frac{1}{x^2+4 x+3}, x \in R, x \neq-3, x \neq-1$ (a) Select the equations of the asymptotes (select all that apply) (a) $x=3$ (b) $x=-1$ (c) $x=-3$ (d) $y=0$ (e) $y=1$
Total Mark	3
Correct Answer	b,c,d
Explanation	na
Mark Scheme	$f(x)=\frac{1}{x^2+4 x+3}=\frac{1}{(x+3)(x+1)}$ Vertical asymptotes: $x=-3, x=-1$ Horizontal aytsmptote: $y=0$ Answer: B, C, D
Question Text	(b) Select the correct coordinates of the local maximum. (a) (2,1) (b) (-2,1) (c) (2,-1) (d) (-2,-1)
Total Mark	3
Correct Answer	d
Explanation	na
Mark Scheme	$\begin{gathered} x^2+4 x+3=(x+2)^2-1 \\ f(x)=\frac{1}{(x+2)^2-1} \end{gathered}$ Local maximum: $(-2,-1)$ Answer: D
Question Text	(c) Hence select the correct graphical representation of $f(x)$

Total Mark	5
Correct Answer	a
Explanation	na
Mark Scheme	na

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source
Question Text	The function f is defined by $f(x) = 3x³ + 4$ where $-2 ≤ x ≤ 2$ (a) What is the range of $f$ ? (a) $0 ≤ f(x) ≤ 4$ (b) $-2 ≤ f(x) ≤ 2$ (c) $-2 ≤ f(x) ≤ 7$ (d) $-20 ≤ f(x) ≤ 28$
Total Mark	2
Correct Answer	d
Explanation	na
Mark Scheme	As $-2 ≤ x ≤ 2$ , lowest is $f(-2),$ and largest is $f(2)$ Thus, $-20 ≤ f(x) ≤$ 28 Answer: (D)
Question Text	(b) Find an expression for $f⁻¹(x)$ . (a) $y=x-4$ (b) $y=x+4$ (c) $y=\sqrt[3]{x-4}$ (d) $y=\sqrt[3]{x+4}$
Total Mark	2
Correct Answer	c
Explanation	na
Mark Scheme	Take the inverse, $x = 3y³ + 4$ $y = \sqrt[3]{x-4}$ Answer: (C)
Question Text	(c) Write down the domain of $f⁻¹$ can be written as $-a ≤ x ≤ b$ where $a, b$ ∈ $Z^+$ . Compute the value of $a + b$
Total Mark	2
Correct Answer	48
Explanation	na
Mark Scheme	The domain of an inverse function is the range of the original function, thus, $-20 ≤ x ≤$ 28 Answer: 48

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes; Irrational; Graph
Source	N16-TZ0-P1-3(HL)
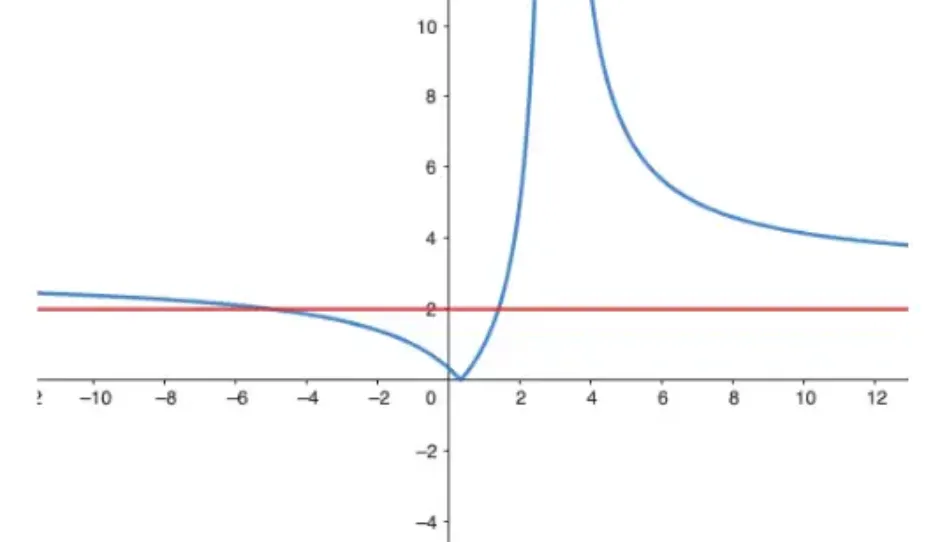
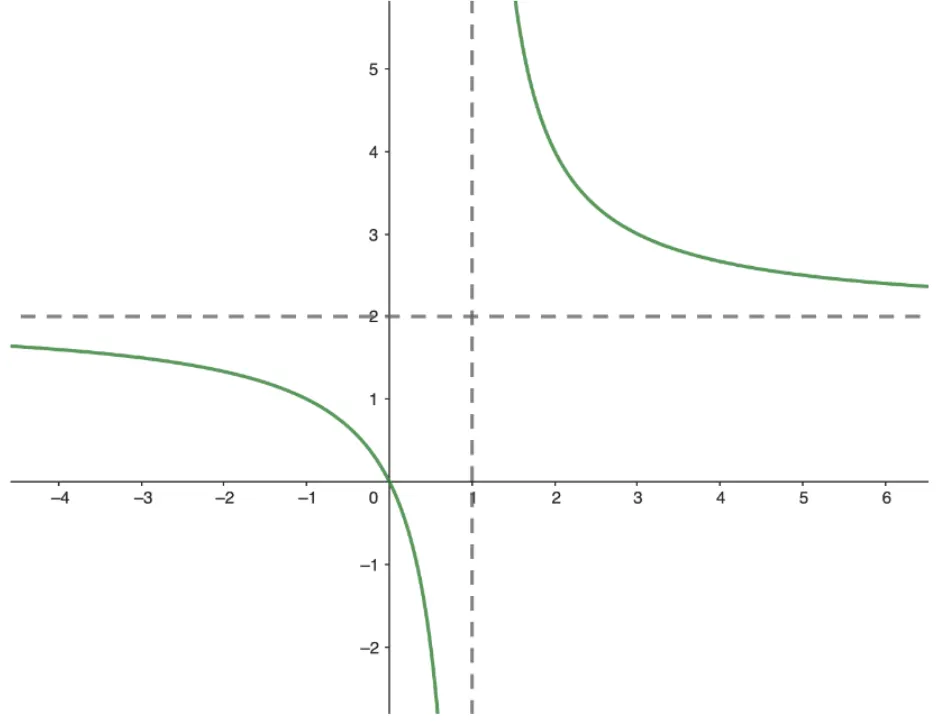
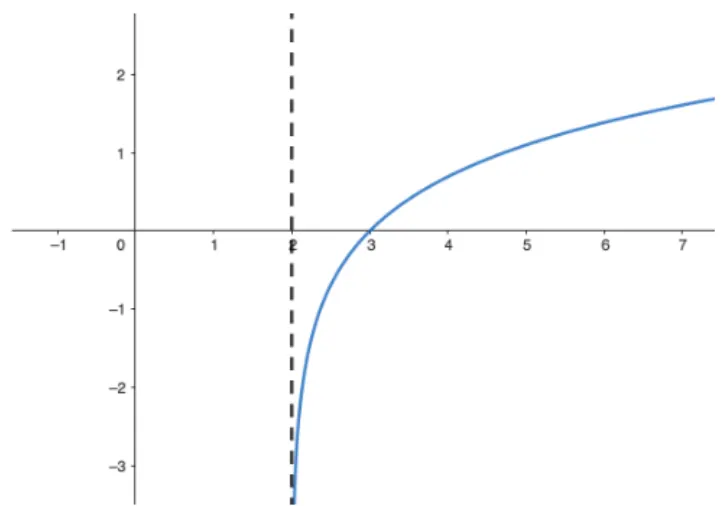
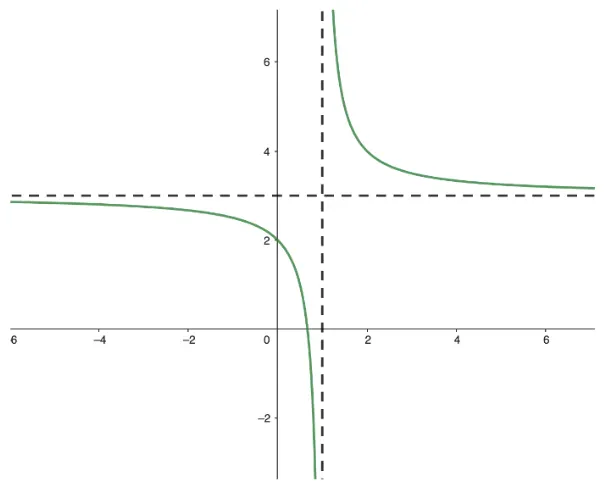
Question Text	A rational function is defined by $f(x)=a+\frac{c}{x-b}$ where $a, b, c \in Z$ and $x \in R$ . The following diagram represents the graph of $y=f(x)$ Using the information on the graph, (a) State the value of $a$

Total Mark	1
Correct Answer	2
Explanation	na
Mark Scheme	Horizontal asymptote is $y=2$ , which represents the value of $a$ Answer: 2
Question Text	(b) State the value of $b$ .
Total Mark	1
Correct Answer	1
Explanation	na
Mark Scheme	Horizontal asymptote is $x = 1$ represented by $b$ Answer: 1
Question Text	(c) Find the value of c.
Total Mark	2
Correct Answer	2
Explanation	na
Mark Scheme	Use the coordinate (0, 0) on the graph, $f(0)$ = 0 2 + $\frac{c}{(0-1)}$ = 0 c = 2 Answer: 2

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes; Irrational; Graph
Source	M16-TZ1-P1-7(HL)
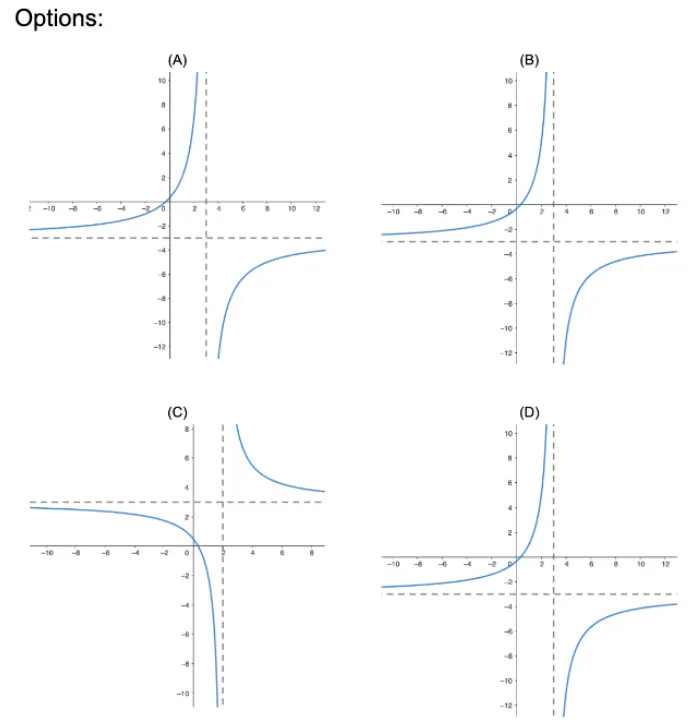
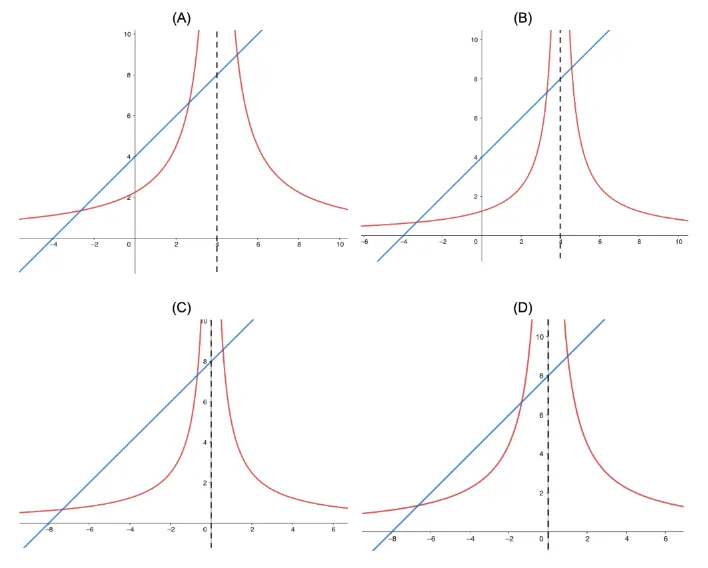
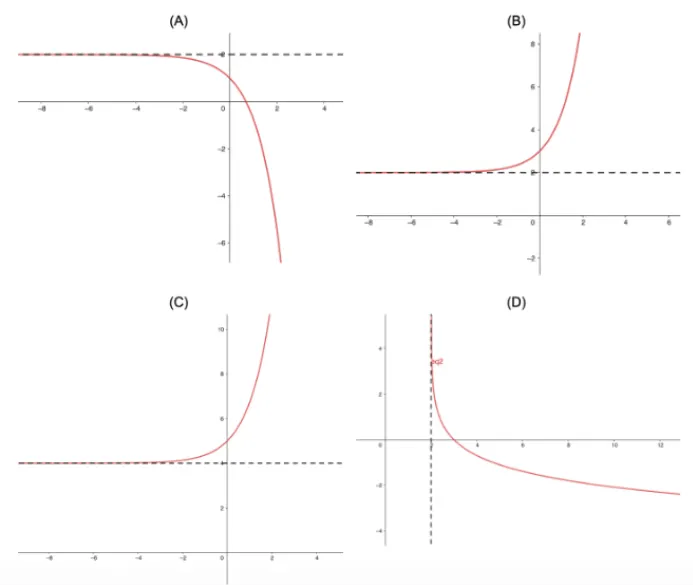
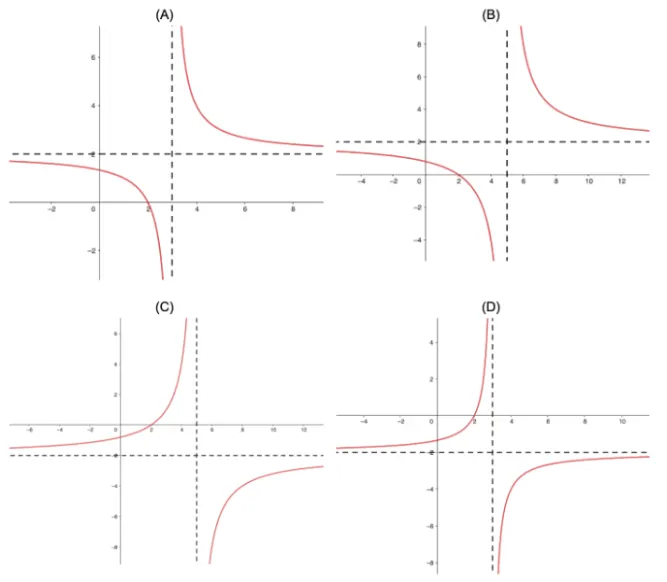
Question Text	(a) Which graph accurately represent the curve $y=\left\|\frac{9}{x-4}\right\|$ and the line $y=x+4$ ? [multiple choice]

Total Mark	3
Correct Answer	(A)
Explanation	na
Mark Scheme	Vertical asymptote: $x = 4$ y-intercept: (0, 4), (0, $\frac{9}{4}$ ) Answer: (A)
Question Text	(b) The equation $x+4=\left\|\frac{9}{x-4}\right\|$ has three unique solutions that can be written as $a, \sqrt{b},-\sqrt{c}$ , where $a, b, c \in \mathbb{Z}^{+}$ . Find $\mathrm{a}+\mathrm{b}+\mathrm{c}$ .
Total Mark	5
Correct Answer	19
Explanation	na
Mark Scheme	The question can be separated into two cases, Case 1: $x>4$ As $\frac{9}{x-4}$ is positive, $\begin{gathered} x+4=\frac{9}{x-4} \\ x^2-16=9 \\ x^2=25 \end{gathered}$ So $x=5$ Case 2: $x<5$ As $\frac{9}{x-4}$ is negative, $\begin{gathered} x+4=-\frac{9}{x-4} \\ x^2-16=-9 \\ x^2=7 \end{gathered}$ So $x= \pm \sqrt{7}$ $a=5$ $b=7$ $\mathrm{c}=7$ Thus, $a+b+c=19$

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source	M16-TZ2-P1-2(HL)
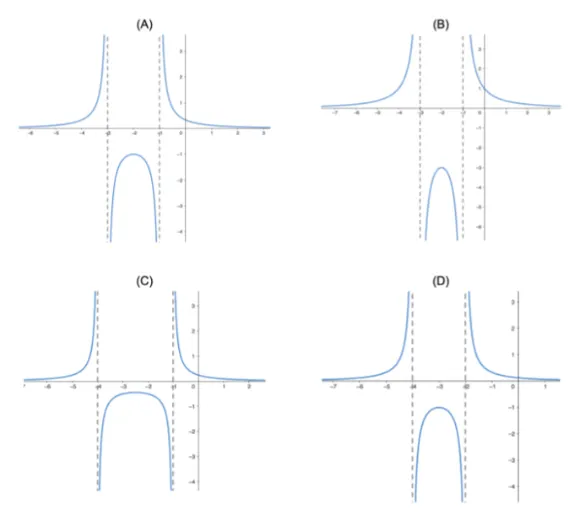
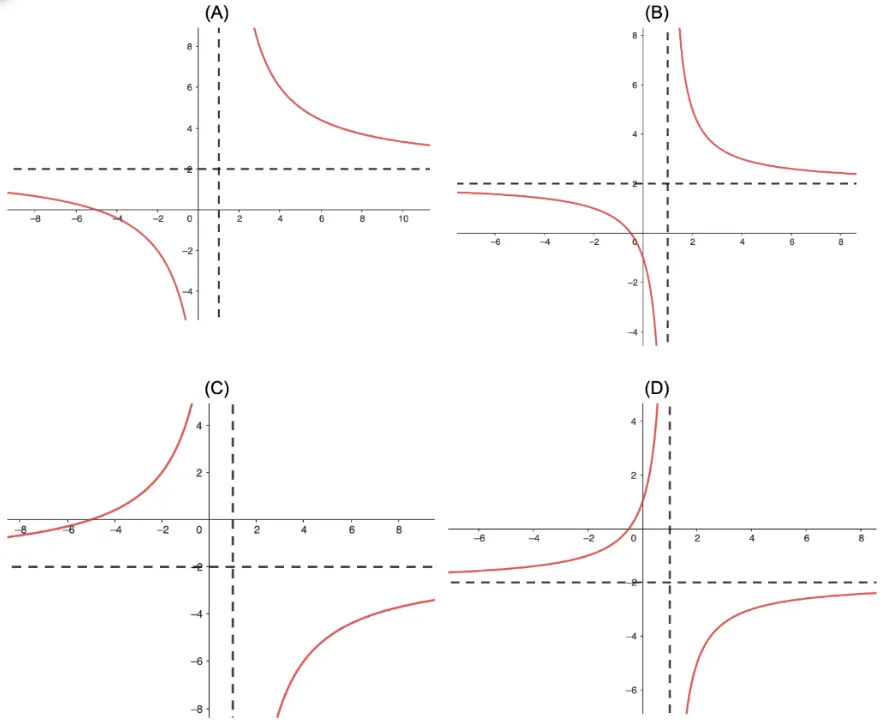
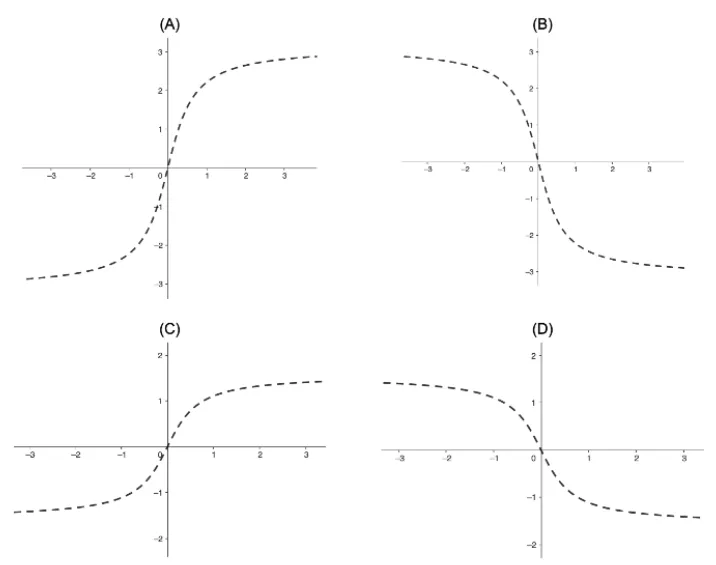
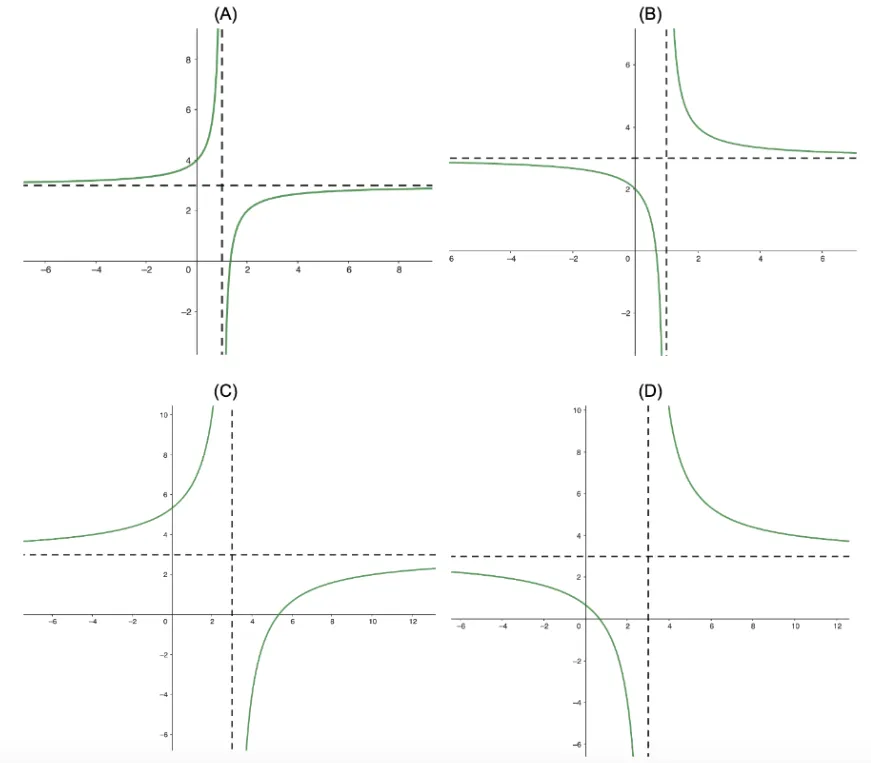
Question Text	The function $f$ is defined as $f(x)=\frac{2 x+1}{x-1}, x \in R, x \neq-1$ . Which graph accurately represents $y=f(x)$ ?

Total Mark	3
Correct Answer	B
Explanation	na
Mark Scheme	Vertical asymptote: $x=1$ Horizontal asymptote: $f(x)=\frac{2 x+1}{x-1}=2+\frac{3}{x-1}$ So, $y=2$ $x$ - intercept: $\begin{gathered} 2 x+1=0 \\ x=-0.5 \end{gathered}$ So, (-0.5,0)

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source	M15-TZ1-P1-5(HL)
Question Text	The functions $f$ and $g$ are defined by $f(x)=a x^4+b x+c, x \in R$ and $g(x)=p \cos x+q x+r, x \in R$ where $a, b, c, p, q, r$ are real constants. (a) Given that $f$ is an odd function, find the value of $a$ .
Total Mark	2
Correct Answer	0
Explanation	na
Mark Scheme	$f(x) = -f(-x)$ $ax⁴ + bx +$ c = $-(a(-x)⁴ + b(-x) + c)$ $2ax$ ⁴ = 0 Thus,a = 0 Answer: 0
Question Text	(b) Given that g is an even function, find the value of $q$ .
Total Mark	2
Correct Answer	0
Explanation	na
Mark Scheme	g(- x) = g(x) p⁡ cos(- x) + qx + r = p cos(- ⁡x) - qx + r As cos x = cos (-x) 2qx = 0 Thus, q = 0 A

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source	N14/5/MATHL/HP1/ENG/TZ0/XX/11a,b
Question Text	The function $f$ is defined as $f(x)=e^{2 x+1}, x \in R$ . (a) Find $f^{-1}(x)$ . (a) $y=e^{\frac{x}{2}-1}$ (b) $y=\frac{e^x}{2}-1$ (c) $y=\ln x-1$ (d) $y=\frac{1}{2}(\ln x-1)$
Total Mark	2
Correct Answer	D
Explanation	na
Mark Scheme	(a) Take the inverse, $\begin{gathered} x=e^{2 y+1} \\ \ln x=2 y+1 \\ y=\frac{1}{2}(\ln x-1) \end{gathered}$ Answer: D
Question Text	(b) The domain of $f⁻¹(x)$ can be written as $x > a$ where $a ∈ ℤ.$ Compute the value of $a$ .
Total Mark	2
Correct Answer	0
Explanation	na
Mark Scheme	As logarithms can’t have a negative value inside, $x >$ 0 Answer: 0
Question Text	The function $g$ is defined as $g(x)=\ln x, x \in R^{+}$ . The graph of $y=g(x)$ and the graph of $y=f^{-1}(x)$ intersect at the point $P$ . (c) Find the coordinates of $P$ (a) $\left(-1, e^{-1}\right)$ (b) $\left(\frac{-3}{4}, e^{\frac{-1}{2}}\right)$ (c) $\left(e^{-1},-1\right)$ (d) $\left(e^{\frac{-1}{2}}, \frac{-3}{4}\right)$
Total Mark	4
Correct Answer	C
Explanation	na
Mark Scheme	Consider the given information, $\begin{gathered} \ln x=\frac{1}{2}(\ln x-1) \\ 2 \ln x=\ln x-1 \\ \ln x=-1 \\ x=e^{-1} \\ y=f^{-1}\left(e^{-1}\right)=\frac{1}{2}\left(\ln e^{-1}-1\right) \\ y=-1 \end{gathered}$ Coordinates of $P$ are $\left(e^{-1},-1\right)$ Answer: C

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source	M14/5/MATHL/HP1/ENG/TZ2/XX/14
Question Text	Consider the following functions: $h(x)=\arctan (2 x), \quad x \in R \quad g(x)=\frac{1}{4 x}, \quad x \in R, \quad x \neq 0$ (a) Which graph accurately represents $y=h(x)$ ?

Total Mark	2
Correct Answer	C
Explanation	na
Mark Scheme	As the range of $arctan(2x)$ is, $-\frac{\pi }{2}$ ≤ $arctan(2x)$ ≤ $\frac{\pi }{2}$ Answer: C
Question Text	Given that $f(x) = h(x) + h∘g(x) = c$ , for some constant $c$ , (b) Find the value $o$ f c. a) 0 b) $\frac{5}{2}$ c) $\frac{\pi }{2}$ d) $\frac{5\pi }{2}$
Total Mark	3
Correct Answer	c
Explanation	na
Mark Scheme	(b) $f(x)=\arctan (2 x)+\arctan \left(\frac{1}{2 x}\right)$ As its given that $f(x)$ is constant $\begin{gathered} f\left(\frac{1}{2}\right)=\arctan (1)+\arctan \\ f\left(\frac{1}{2}\right)=\frac{\pi}{4}+\frac{\pi}{4} \\ f\left(\frac{1}{2}\right)=\frac{\pi}{2} \end{gathered}$ Thus $c=\frac{\pi}{2}$ Answer: C
Question Text	Nigel states that f is an odd function and Tom argues that $f(x)$ is an even function. (c) By considering whether the $f(x)$ is an odd function or an even function, find the value of $f(x)$ for $x < 0$ . a) 0 b) $-\frac{5}{2}$ c) $-\frac{\pi }{2}$ d) $\frac{5\pi }{2}$
Total Mark	3
Correct Answer	C
Explanation	na
Mark Scheme	$\begin{gathered} \text { (c) } f(-x)=\arctan (-2 x)+\arctan \left(\frac{-1}{2 x}\right) \\ f(-x)=-\arctan (2 x)-\arctan \left(\frac{1}{2 x}\right) \\ f(-x)=-f(x) \end{gathered}$ therefore $f$ is an odd function Thus, $f(x)=-\frac{\pi}{2}$ when $x<0$ Answer: C

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source	N13-TZ0-P1-3(HL)
Question Text	The diagram below shows a sketch of the graph of $y=f(x)$ .

a) Which graph represents

y=f^{-1}(x)

?

Total Mark	2
Correct Answer	B
Explanation	na
Mark Scheme	Mirror with regards to $y = x$ .
Question Text	(b) The range of $f⁻¹(x)$ can be written as $f⁻¹(x) > k$ where $k$ ∈ $ℤ^+$ . Compute the value of $k$ .
Total Mark	1
Correct Answer	2
Explanation	na
Mark Scheme	Range is $f⁻¹(x) >$ 2 Answer: 2
Question Text	(c) Given that $f(x) = ax - b$ , $x > 2$ , $a,b$ ∈ $ℤ^+$ (i) find the value of $a$ Total Mark : 2 Correct Answer: 1 Explanation: na Mark Scheme: na (ii) Find the value of $b$ . Total Mark: 2 Correct Answer: 2 Explanation: na Mark Scheme : $x$ -intercept: $(3,0)$ $ln⁡(3a - b)$ = 0 $3a - b = 1$ Asymptote at $x$ = 2 $2a - b$ = 0 $a$ = 1, $b$ = 2 (i) Answer: 1 (ii) Answer: 2

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source	M13-TZ2-P1-9(HL)
Question Text	The function $f$ is given by $f(x)=\frac{2^x+1}{2^x-2^{-x}}$ , for $x>0$ . The solution to the equation $f(x)=3$ can be written as $\log _2\left(\frac{a}{b}\right)$ where $a$ and $b$ are positive integers in lowest terms. Find the value of $a+b$ . [4]
Total Mark	4
Correct Answer	5
Explanation	na
Mark Scheme	$\begin{gathered} \frac{2^x+1}{2^x-2^{-x}}=3 \\ 2^x+1=2\left(2^x-2^{-x}\right) \\ 2 \times 2^{2 x}-2^x-3=0 \end{gathered}$ Use the substitution $y=2^x$ $\begin{gathered} 2 y^2-y-3=(2 y-3)(y+1) \\ y=\frac{3}{2} \end{gathered}$ Thus, $x=\log _2\left(\frac{3}{2}\right)$ Answer: 5

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source	N19/5/MATHL/HP1/ENG/TZ1/XX/10 b,c
Question Text	$\operatorname{Consider} f(x)=\frac{2 x-8}{x^2-4},-2<x<2$ (a) For the graph of $y=f(x)$ , (i) Find the $y-$ coordinate of the $y-$ intercept Total Mark: 1 Correct Answer: 2 Explanation: na Mark Scheme: $f(0)=2$ Answer: 2 (ii) Find the number of $x$ -intercepts. Total Mark: 2 Correct Answer: 2 Explanation: na Mark Scheme: $2x - 10 = 0$ $x = 5$ Outside the domain so no $x$ -intercepts. Answer: 0 (iii) Which graph accurately represents $y=f(x)$ ?

Total Mark: 2 Correct Answer: B Explanation: na Mark Scheme: na

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source	M19/5/MATHL/HP1/ENG/TZ2/XX/5
Question Text	(a) Select the graph of y=2x−4x−3y=\frac{2 x-4}{x-3}y=x−32x−4

Total Mark	5
Correct Answer	A
Explanation	na
Mark Scheme	na
Question Text	(b) Consider the function $f(x)=\sqrt{\frac{2 x-4}{x-3}}$ . The domain of $f$ can be written as $x \leq a, x>b$ for integers $a$ and $b$ . Write down (i) the value of $a$ Total mark : 1 Correct Answer: 2 Explanation: na Mark Scheme: na (ii) the value of $b$ Total Mark: 1 Correct Answer: 3 Explanation: na Mark Scheme: $f(x) > 0$ By considering the graph, $x ≤ 2$ , $x > 3$ (i) Answer: 2 (ii) Answer: 3

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source	M19/5/MATHL/HP1/ENG/TZ2/XX/9 a
Question Text	Consider the functions $f$ and $g$ defined on the domain $0<x<\frac{\pi}{2}$ by $f(x)=3 \cos 2 x$ and $g(x)=4-11 \cos x$ The $x$ -coordinate of the point of intersection of the two graphs can be written as $\sin ^{-1}\left(\frac{a}{b}\right)$ where $a$ and $b$ are integers in lowest terms. Compute the value of $a+b$ .
Total Mark	6
Correct Answer	4
Explanation	na
Mark Scheme	Equate the functions to find the intersection point, $3 \cos 2 x=13 \sin x-2$ Using the double angle identity for cos $\begin{gathered} 3\left(1-2 \sin ^2 x\right)=13 \sin x-2 \\ 6 \sin ^4 x+13 \sin x-5=0 \\ (3 \sin x-1)(2 \sin x+5)=0 \\ \sin x=\frac{1}{3} \\ x=\sin ^{-1}\left(\frac{1}{3}\right) \end{gathered}$ Answer: 4

Topic	2.1 Functions
Tag	Functions; Domain; Range; Composite functions; Inverse functions; Reciprocal functions; Asymptotes ; Irrational; Graph
Source	M18/5/MATHL/HP1/ENG/TZ2/XX/10
Question Text	The function $f$ is defined by $f(x)=\frac{a x+b}{c x+d}$ , for $x \in R, x \neq-\frac{d}{c}$ . (a) Find the inverse function $f^{-1}$ Options: (A) $f^{-1}(x)=\frac{c x+d}{a x+b}$ (B) $f^{-1}(x)=\frac{c x-d}{a-b x}$ (C) $f^{-1}(x)=\frac{d x+b}{c x+a}$ (D) $f^{-1}(x)=\frac{d x-b}{a-c x}$
Total Mark	3
Correct Answer	D
Explanation	na
Mark Scheme	(a) Take the inverse, $\begin{gathered} x=\frac{a y+b}{c y+d} \\ x(c y+d)=a y+b \\ y(a-c x)=d x-b \\ y=\frac{d x-b}{a-c x} \end{gathered}$ Answer: (D)
Question Text	(b) State the domain of $f^{-1}$ (A) $x \neq \frac{-b}{a}, x \in R$ (B) $x \neq \frac{a}{b}, x \in R$ (C) $x \neq \frac{-a}{c}, x \in R$ (D) $x \neq \frac{a}{c}, x \in R$
Total Mark	1
Correct Answer	D
Explanation	na
Mark Scheme	$a - cx ≠ 0$ $x ≠ a/c , (x∈R)$ Answer: (D)
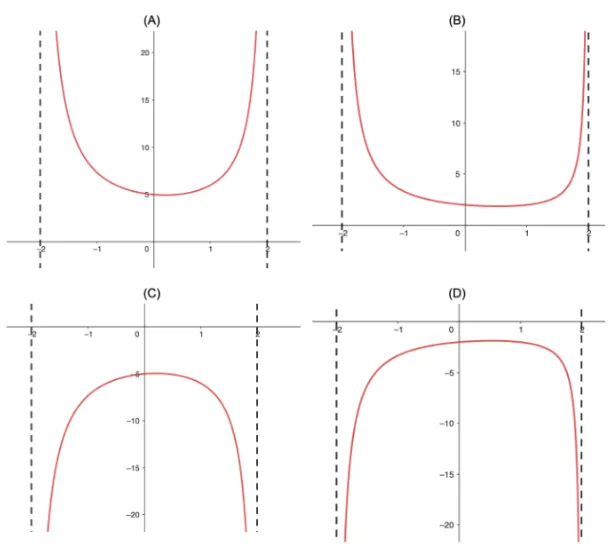
Question Text	The function g is defined by $g(x)=\frac{3 x-2}{x-1}, x \in R, x \neq 2$ . (c) i. $\quad g(x)$ can be written in the form $A+\frac{B}{x+1}$ where $A, B$ are constants. Compute the value of $A+B$ . Total Mark: 2 Correct Answer: 4 Explanation: na Mark Scheme: $g(x)=\frac{3(x-1)+1}{x-1}=3+\frac{1}{x-1}$ Answer: 4 ii. Sketch the graph of $y=g(x)$ . State the equations of any asymptotes and the coordinates of any intercepts with the axes. [multiple choice]

Total Mark: 3 Correct Answer: B Explanation: na Mark Scheme:

Vertical asymptote

x=1

Horizontal asymptote

y=3

y

-intercept

(0,2)

Answer: B

2.1 Functions

Q1

Q2

Q3

Q4

Q5

Q6

Q7

Q8

Q9

Q10

Q11

Q12

Q13

Q14

Q15

Q16