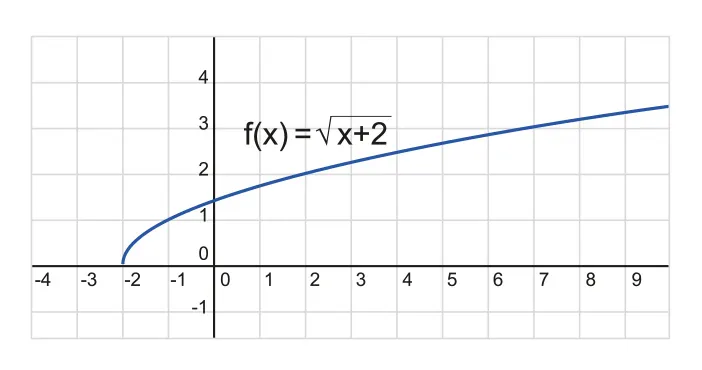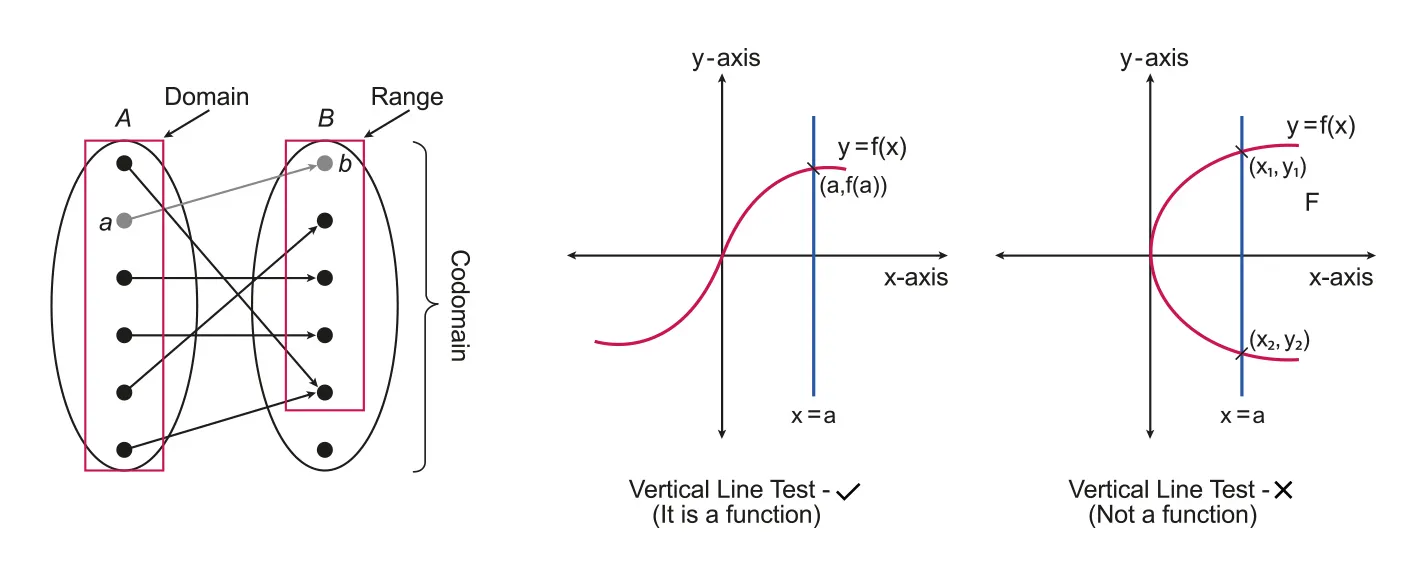
2.1 Functions

Function has different properties:

Domain is the set of values of xxx in the relation. (the set XXX )

Range is the set of values of yyy in the relation. (the set YYY )

Function must pass the vertical line test.

Allowed maximum one intersection with vertical lines across the real axis

Multiple inputs →\rightarrow→ one input (ok)

One input →\rightarrow→ multiple output (no)

Function notation: f:X→Y, x↦x+3f: X → Y,  x ↦ x+3f:X→Y, x↦x+3

Domain and Range are written in set notation; ex. {x∣2<x<4x | 2<x<4x∣2<x<4},   x∈[1,3)x ∈[1, 3)x∈[1,3)

Colored dot = inclusive; empty dot = exclusive

All real number; ex. domain: {x∣x∈Rx | x∈ ℝx∣x∈R}

Substitute x=0x = 0x=0 to obtain yyy intercept, and vice versa.

Figure 2.1.1 Function can be one-to-one (bijective)

A bijective function, one-to-one correspondence, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other set, and each element of the other set is paired with exactly one element of the first set; there are no unpaired elements between the two sets.

One-to-one function must pass the horizontal line test

Allowed maximum one intersection with horizontal lines across the real axis

Multiple inputs →\rightarrow→ one input (no)

One input →\rightarrow→ multiple output (no)

One-to-one functions are either always increasing or decreasing across their entire domain.

Function can be even or odd.

Even function is invariant under a reflection in the y axis: f(x)=f(−x)f(x)=f(-x)f(x)=f(−x)

Odd function has rotational symmetry about the origin: f(x)=−f(−x)f(x)=-f(-x)f(x)=−f(−x)

Composite Functions

Given functions

f: x ↦ f(x)

and

g: x ↦ g(x)

, the composite function of

f

and

g

will convert into

f(g(x))

(f\cdot g)(x)

is used to represent the composite function of

f

and

g

. It means

f

following

g

(f\cdot g)(x) = f(g(x))

f\cdot g :x ↦ f(g(x))

Note that:

Not commutative; (f⋅g)(x)≠(g⋅f)(x)(f\cdot g)(x) ≠ (g\cdot f)(x)(f⋅g)(x)=(g⋅f)(x)

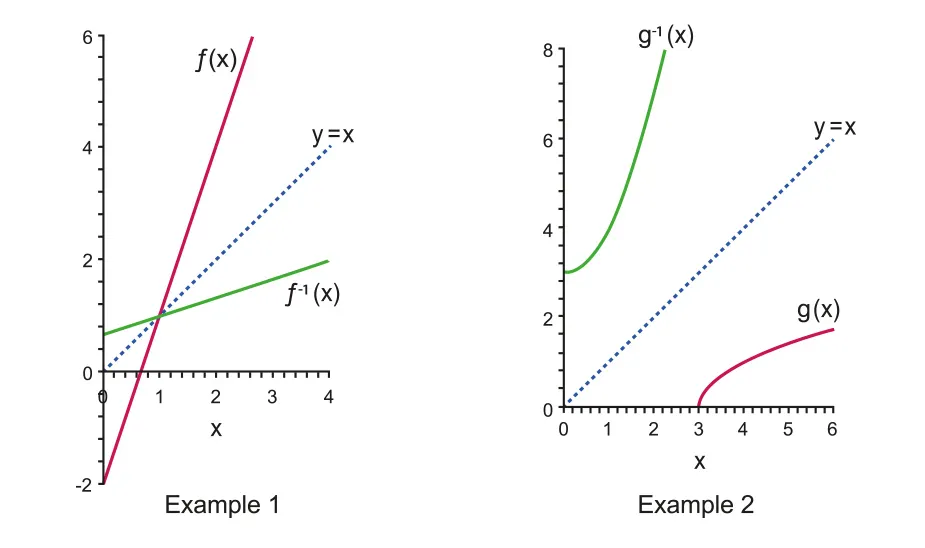
Associative; f⋅g⋅h=f⋅(g⋅h)=(f⋅g)⋅hf \cdot g \cdot h =f \cdot (g \cdot h) = (f \cdot g) \cdot hf⋅g⋅h=f⋅(g⋅h)=(f⋅g)⋅h

Inverse Functions

A function must be one-to-one (bijective) for it to have an inverse. We denote inverse of

f

to be

f^{-1}

and they are an inverse operation of each other; i.e.

f(a) = b

then

f^{-1}(b) = a

Below are some properties of inverse function:

Domain of fff becomes the range of f−1f^{-1}f−1, and vice versa.

They are symmetric about the identify function; i.e. the line y=xy = xy=x.

f(f−1(x))=f−1(f(x))=xf(f^{-1}(x)) = f^{-1}(f(x)) = xf(f−1(x))=f−1(f(x))=x

A function that has itself as an inverse is called the self-inverse function.

You calculate the inverse by the following steps:

Isolate in terms of xxx

Swap xxx and yyy; i.e. xxx becomes yyy and vice versa.

Replace yyy to be f−1(x)f^{-1}(x)f−1(x) where appropriate.

Figure 2.1.2 The symmetry of inverse functions about the line

y=x

Asymptotes

A line where the graph gets arbitrarily close at a singular point or infinity, but never succeeds to reach.

There are two types:

Vertical asymptote: x=kx = kx=k

Horizontal asymptote: y=ky = ky=k

To identify asymptotes, investigate possible points of singularities or check limits at infinity.

Rationals

General form:

y = \frac{cx + d}{ax + b}

Standard form:

y = \frac {c}{ax + b}+d

From the standard form, we have:

Horizontal asymptote: y=dy = dy=d

Vertical asymptote: x=−bax = -\frac {b}{a}x=−ab​

For the sign of ccc,

c>0c > 0c>0 then hyperbola in the top right and bottom left

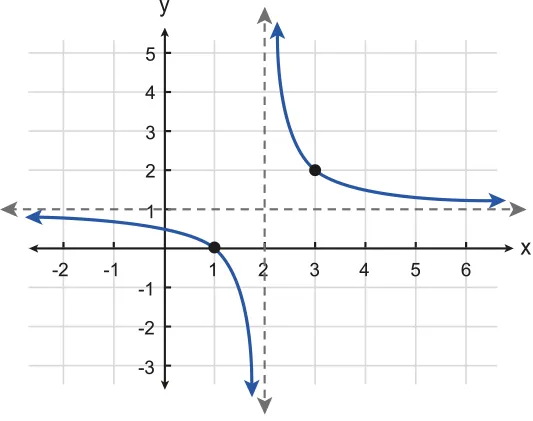
Figure 2.1.3 Rational function :

y=\frac{1}{x-2}+1

c<0c < 0c<0 then hyperbola in the top left and bottom right

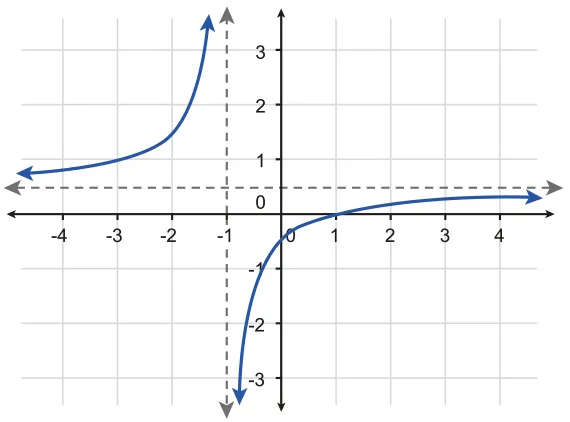
Figure 2.1.4 Rational function :

-\frac{1}{x+1}+\frac{1}{2}

Domain: {x∣x≠−bax | x ≠- \frac bax∣x=−ab​}

Range: {y∣y≠dy | y ≠ dy∣y=d}

Quickest way to draw this function:

Convert general form to the standard form.

Locate the asymptotes, then find the intercepts.

Graph the hyperbola accordingly with the sign of ccc.

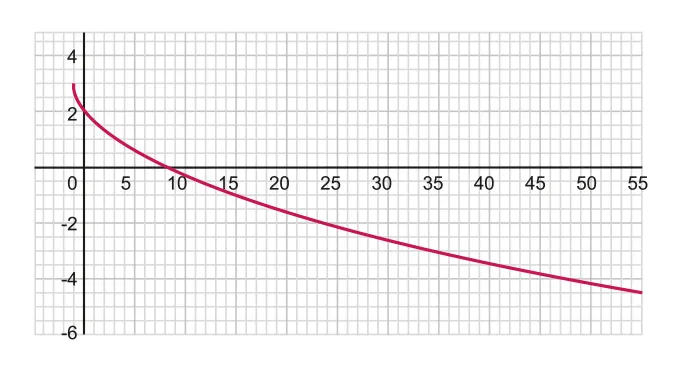
Irrationals

General form:

y = a \sqrt {bx + c}+d

From the general form, we have:

Starting point of the function: (−cb,d)- \frac c b, d)−bc​,d)

Domain ={x∣x≥−cbx | x ≥ - \frac cbx∣x≥−bc​}; i.e. the expression inside the root must be greater than equal to 0.

For the sign of aaa,

a>0a > 0a>0: Range ={y∣y≥dy | y ≥ dy∣y≥d}

a<0a < 0a<0: Range ={y∣y≤dy | y ≤ dy∣y≤d}

Quickest way to draw this function:

Locate the starting point.

Graph the function according to the domain and range. This function is a monotonically increasing/decreasing function.

Figure 2.1.5 Irrational function with a positive coefficient

Figure 2.1.6 Irrational function with a negative coefficient

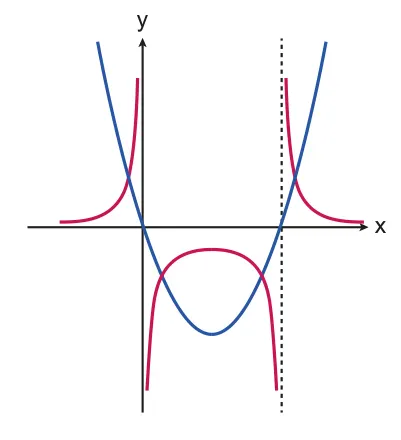
Reciprocal functions (HL)

General form:

\frac 1{f(x)}

, or

[f(x)]^{-1}

From the general form, we have:

f(x)→0+⇔1f(x)→∞,f(x)→0−⇔1f(x)→−∞f(x) \rightarrow 0^+ \Leftrightarrow \frac1{f(x)} \rightarrow ∞, f(x) \rightarrow 0^- \Leftrightarrow \frac 1{f(x)} \rightarrow-∞f(x)→0+⇔f(x)1​→∞,f(x)→0−⇔f(x)1​→−∞

f(x)→∞⇔1f(x)→0+,f(x)→−∞⇔1f(x)→0−f(x) \rightarrow ∞ \Leftrightarrow \frac 1{f(x)} \rightarrow 0^+, f(x) \rightarrow -∞ \Leftrightarrow \frac 1{f(x)} \rightarrow 0^-f(x)→∞⇔f(x)1​→0+,f(x)→−∞⇔f(x)1​→0−

Local minimum of f(x)f(x)f(x) becomes the local maximum of [f(x)]−1[f(x)]^{-1}[f(x)]−1

Local maximum of f(x)f(x)f(x) becomes the local minimum of [f(x)]−1[f(x)]^{-1}[f(x)]−1

Zeroes of f(x)f(x)f(x) become the vertical asymptotes of [f(x)]−1[f(x)]^{-1}[f(x)]−1

The point (a,ba, ba,b) translates to (a,1ba,\frac 1ba,b1​)

The sign of the original function is preserved.

Figure 2.1.7 Relationships between reciprocal functions

2.1 Functions

done

https://docs.google.com/forms/d/e/1FAIpQLSd2Ywy5r6vcLD-Gg9FTVFE_ighR3FJVomlrSgpSvdbmd3bx6w/viewform

2.1 Functions