C.1 Simple Harmonic Motion

생성일

2024/07/05 08:37

태그

C.1.1 Simple harmonic oscillations and its conditions

Oscillation: periodic motions which center around an equilibrium position

Wave: transfer of energy without transfer of matter

Simple harmonic motion (SHM): motion in which the restoring force (acceleration) is directly proportional to the displacement of the body from its equilibrium point

•

Period and amplitude are constant

•

Period is independent of amplitude

•

Sinusoidal (can be represented into sine or cosine graph)

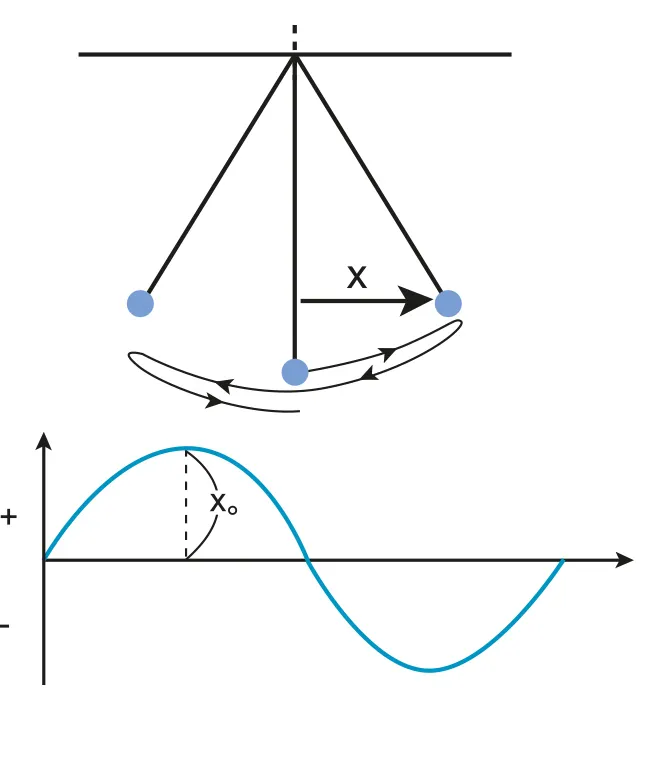
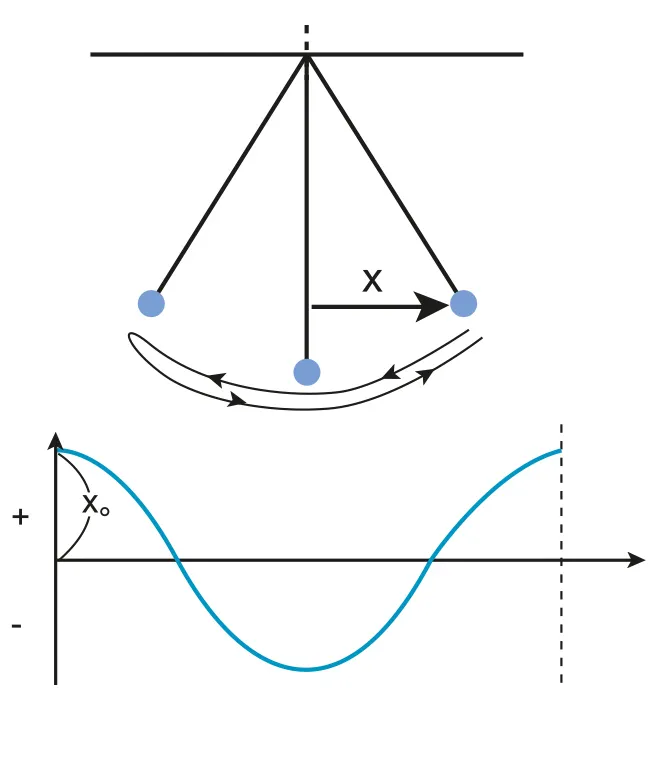
C.1.1-1 2D diagrams and graphs that represents SHM in pendulum

Condition for simple harmonic motion:

•

A restoring force is required for simple harmonic motion to occur

◦

A restoring force is a force directed towards the equilibrium position such that if the object is moved away from its equilibrium position, it will always be ‘pushed’ back towards that point.

•

Magnitude of restoring force is proportional to displacement and acts towards the equilibrium

F ∝-x, F=-kx (k=spring constant)

Since\, F=ma,

-kx=ma,a= -\frac kmx

∴ a ∝-x

*The negative sign indicates that the acceleration always points towards the equilibrium.

C.1.1-2 Graph representing the relationship between acceleration and displacement in SHM

Angular Velocity

•

Vector measure of the rotation rate, which refers to how fast an object rotates or revolves relative to another point

•

Used for the relationship between restoring force and equilibrium in SHM

C.1.1-3 Diagram of angular velocity with notations

\omega = \frac{\theta}{t}\\ \theta = 2\pi, \quad t = T \quad (T = \textit{period})\\ \omega = \frac{2\pi}{T}\\ f = \frac{1}{T} \quad (f = \textit{{frequency}})\\ \omega = 2\pi f

Proof of Simple Harmonic Motion with Sine / Cosine graph

Sine Graph

C.1.1-4 Sine graph

C.1.1-5 Cosine graph

(x_0 = \textit{maximum displacement}, \quad \omega = \textit{angular velocity})\\ x = x_0 \cdot \sin(\omega t)\\ v = \frac{dx}{dt} = x_0 \cdot \omega \cdot \cos(\omega t)\\ a = \frac{dv}{dt} = - x_0 \cdot \omega^2 \cdot \sin(\omega t)\\ \text{Since} \quad x = x_0 \cdot \sin(\omega t)\\ a = -\omega^2 \cdot x

(x_0 = \textit{maximum displacement}, \quad \omega = \textit{angular velocity})\\ x = x_0 \cdot \cos(\omega t)\\ v = \frac{dx}{dt} = - x_0 \cdot \omega \cdot \sin(\omega t)\\ a = \frac{dv}{dt} = - x_0 \cdot \omega^2 \cdot \cos(\omega t)\\ \text{Since} \quad x = x_0 \cdot \cos(\omega t)\\ a = -\omega^2 \cdot x

•

So, the acceleration is directly proportional to negative displacement and is always directed towards equilibrium

C.1.1-5 Cosine graph

Simple Pendulum

•

Point mass hanging on a string/rod with negligible mass

C.1.1-6 Pendulum free body diagram with notations

F = ma\\ mg \sin(\theta) = ma\\ \text{Since}\,\sin(\theta) = \frac{x}{L} \,(x = \textit{displacement}, \,l = \textit{radius of pendulum})\\ mg \left(\frac{x}{L}\right) = ma\\ g \left(\frac{x}{L}\right) = a\\ \text{Since}\,a = - \omega^2 \cdot x\\ - \omega^2 \cdot x = - g \left(\frac{x}{L}\right)\\ \omega^{2} = \frac{g}{L}\\ \frac{4\pi^2}{T^2} = \frac{g}{L}\\ T^2 = 4\pi^2 \cdot \frac{g}{L}\\ T = 2\pi \sqrt{\frac{L}{g}}\\ T=period, L=length of string/rod, g=gravitational acceleration≈9.81ms^{-2}

Spring-Mass System

C.1.1-7 Diagrams representing SHM in spring

F_{\text{spring}} = -kx \quad (k = \textit{spring constant})\\ \text{Since} \quad F_{\text{weight}} = F_{\text{spring}}\\ ma = - kx\\ \text{Since} \, a = - \omega^2 \cdot x\\ m(-\omega^2 \cdot x) = - kx m \omega^2 = k\\ m \left(\frac{4\pi^2}{T^2} \right) = k\\ T^2 = 4\pi^2 \cdot \left(\frac{m}{k} \right)\\ T = 2\pi \sqrt{\frac{m}{k}}\\ T = \textit{period}, \quad m = \textit{mass}, \quad k = \textit{spring constant}

⇒ for both two examples, it can be observed that period is independent of the amplitude

C.1.2 Time period, frequency, amplitude, displacement and phase difference

Definitions of key terminologies

Terminology	Definition
displacement, x	instantaneous distance from equilibrium with direction (change in position); [m]
amplitude, A	maximum displacement from the mean position (fixed average point); [m]
frequency, f	number of oscillations done per unit time; [Hz = s-1] (cycles per second)
period, T	time taken for one complete oscillation; [s] $T=\frac1f$
phase difference,	difference in phase angle of two waves; [rad] or [°] (deg) • in phase ⇒ $\phi=0$ • out of phase ⇒ $\phi=\pi$ or 180° (half a cycle) • one complete cycle is $2\pi$ or 360°

C.1.3 Graphs of simple harmonic motion

Acceleration, velocity, and displacement during SHM

C.1.3-1 variation of graphs that represent acceleration, velocity and displacement in SHM

•

acceleration leads velocity by 90° (=π2=\frac \pi2
=2π​)

◦

velocity lags acceleration by 90°

•

velocity leads displacement by 90°

◦

displacement lags velocity by 90°

•

acceleration and displacement are 180° out of phase ( ϕ=π or\phi=\pi \,or
ϕ=πor 180°)

Energy changes during simple harmonic motion

•

Energy is interchanged between kinetic energy (KE) and potential energy (PE) (or elastic potential energy, EPE).

∴ maximum value of KE or PE only can be total energy

E_{total}

•

Assuming no resistive forces are applied to dissipate energy, total energy always remains constant.

◦

Such oscillation is said to be undamped.

C.1.3-2 Straight line graph that represents the SHM

Energy in SHM is proportional to:

•

mass, mmm

•

amplitude2,A2amplitude^{2}, A^{2}amplitude2,A2

•

frequency2,f2frequency^{2}, f^{2}frequency2,f2

C.1.3-3 Variation of graphs that represents the KE, PE and total Energy

Time	Energy
$t=0$	$x=x_{max}=x_0 (x_0=A)$ • $KE=0$ • $EPE=\frac12kA2=\frac12kx_0^2$ • $E_{total}=KE+EPE=0+\frac12kA^2=\frac12kA^2$
$t=\frac 14T$	$x=0$ • $EPE=\frac12kx^{2}=\frac12k0^2=0$ • $E_{total}=KE+EPE=\frac12mv_{max}^2+0=\frac12kA^2$ • $v_{\text{max}} = \sqrt{\frac{k}{m} A^2}$
$at\, any\, point\, x$	• $EPE=\frac12kx^2$ • $E_{total}=KE+EPE=0+\frac12kx^2=\frac12kA^2$ • $KE=\frac12kA^2-\frac12kx^2=\frac12mv^2$

C.1.4 Equation of SHM

Simple Harmonic Motion

•

Simple Harmonic Motion : A type of oscillation in which the acceleration on a body is proportional to its displacement, but acts in the opposite direction

a \alpha -x

•

The conditions for an object to oscillate in SHM are that it shows :

◦

Periodic oscillations

◦

Acceleration proportional to its displacement

◦

Acceleration in the opposite direction to its displaceme

C.1.4-1 Diagram of pendulum example of SHM

•

The relationship between the acceleration and displacement in simple harmonic motion can be defined by equation :

a = -\omega^2 x

(a=acceleration,\omega =angular velocity, x=displacement)

•

The equation shows the relationship between acceleration and displacement during simple harmonic motion :

◦

The acceleration reaches its maximum value when the displacement is at a maximum

◦

The minus sign shows that when the object is displacement to the right, the direction of the acceleration is to the left

Mathematic approach of SHM

•

When the graph of acceleration against displacement graph constructed we can notice that the graph shows straight line

C.1.4-2 annotated graph of acceleration and displacement in SHM

•

This shows that the acceleration of an object in simple harmonic motion is opposite but directly proportional to the negative displacement

•

The displacenemt, velocity and acceleration of object during simple harmonic motion can be represent by sin, cos and negative sin graph due to the calculus

C.1.4-3 Chart of graphs in SHM

C.1.4-4

C.1.5 Energy Changes in SHM

Energy Changes in Simple Harmonic Motion

•

During SHM, energy transition happens constantly between kinetic energy and potential energy

•

For kinetic energy :

◦

Maximum when the displacement is zero

◦

This is because kinetic energy can be calculated by

◦

12mv2 and the velocity is maximum when displacement is zero so gains maximum kinetic energy when displacement is zero

•

For potential energy :

◦

Maximum when displacement is maximum

◦

This is because all the kinetic energy is transferred to potential energy as the height above the equilibrium position increases

C.1.5-1 annotated diagram of pendulum

•

For total energy :

◦

Remains constant during SHM

◦

Because total energy is addition of kinetic energy and potential energy and the transition between kinetic energy and potential energy constantly happens during SHM so the total energy remains constant

C.1.5-2 Combined graph with diagram of energy transition of pendulum SHM