C.5.1 The Doppler Effect
The Doppler effect
•
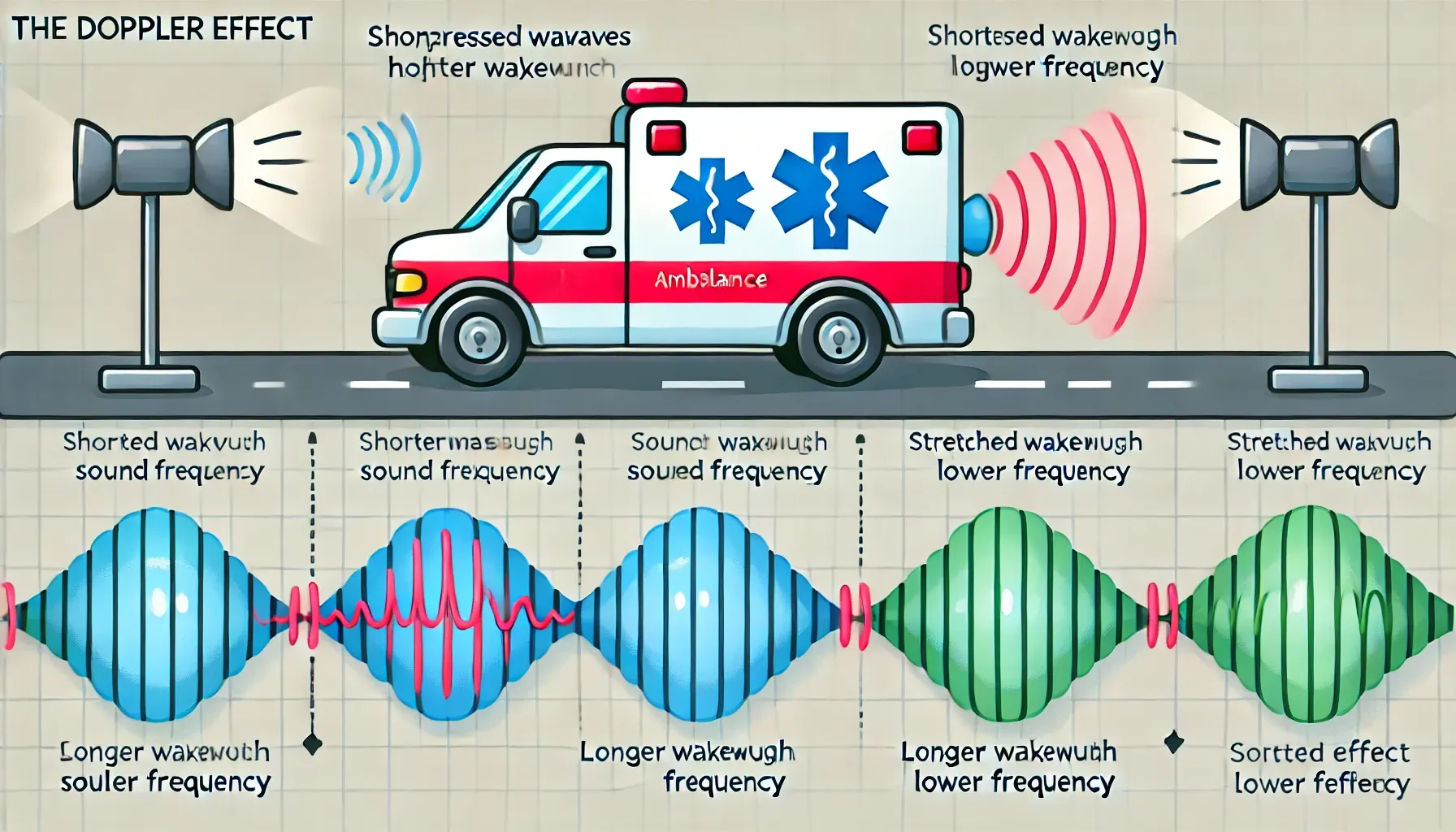
When a source of sound, such as the whistle of a train or the siren of an ambulance, moves away from an observer :
◦
It appears to decrease in frequency, i.e. it sounds lower in pitch
◦
Although, the source of the sound remains at a constant frequency
•
When the observer and the source of wave are both stationary :
◦
The waves appear to remain at the same frequency for both the observer and the source
C.5.1-1 Diagram of doppler effect (stationary)
•
When the source starts to move towards the observer, the wavelength of the waves is shortened
◦
The sound, therefore, appears at a higher frequency to the observer
C.5.1-2 Diagram of doppler effect (moving source)
Redshift/Blueshift of EM Radiation
•
In space the Doppler effect of light can be observed when spectra of distant stars and galaxies are observed, this is known as :
◦
Redshift if the object is moving away from the Earth
◦
Blueshift if the object is moving towards the Earth
C.5.1-3 Diagram of redshift
•
Redshift : The fractional increase in wavelength due to the source and observer receding from each other
•
Doppler redshift can be defined with equation :
C.5.2 The Doppler Equation
Doppler Equation
•
When a source of sound waves moves relative to a stationary observer, the observed frequency can be calculated using the equation below :
•
The ± depends on whether the source is moving towards or away from the observer
◦
If the source is moving towards the observer, the denominator is v - u
◦
If the source is moving away from the observer, the denominator is v + u
•
the observer is moving relative to the source, the observed frequency can be calculated using the equation below :
•
The ± depends on whether the observer is moving towards or away from the source
◦
If the observer is moving towards the source, the numerator is v + u
◦
If the observer is moving away from the source, the numerator is v − u