2.2 Exponents and Logarithms

Tags

Exponents

Logarithms

Graph

Asymptotes

Domain

Range

Functions

Exponential rules

Logarithm rules

Exponential is an inverse operation of logarithm; i.e.

a^x=b ⇒ x = \log_ ab

Therefore, exponential function and logarithm function are an inverse of each other.

Exponentials:

There are few exponential rules to be aware of:

•

am⋅an=am+na^m · a^n = a^{m+n}am⋅an=am+n

•

aman=am−n\frac {a^m}{a^n}=a^{m-n}anam​=am−n

•

anm=anma^{\frac nm}= \sqrt [m] {a^n}amn​=man​

•

a−n=1ana^{-n}=\frac 1{a^n}a−n=an1​

Treat the exponentials like a variable in factorization and expansion.

For the general form

f(x) =k · a^{bx+c}+d

, we have:

Horizontal asymptote: y=dy=dy=d

Vertical asymptote: x=−cbx=-\frac cbx=−bc​

Domain: {x∣x∈Rx | x∈ ℝx∣x∈R}

For the sign of kkk, the range changes:

k>0k>0 k>0 ⇒ {y∣y<dy | y <dy∣y<d}

k<0k<0 k<0 ⇒ {y∣y>dy | y > dy∣y>d}

To solve exponential equations, equate the exponents with the same base numbers.

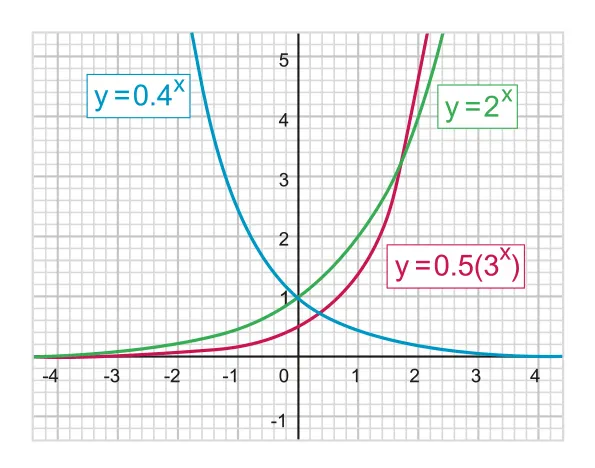
Figure 2.3.1 Exponential functions with different base values

Logarithms

There are few logarithm rules to be aware of:

log⁡ab+log⁡ac=log⁡abc\log _ab+\log_ac=\log _abcloga​b+loga​c=loga​bc

log⁡ab−log⁡ac=log⁡abc\log_ab-\log_ac=\log_a{\frac bc}loga​b−loga​c=loga​cb​

log⁡ab=log⁡cblog⁡ca\log_ab=\frac{\log_cb}{\log_ca}loga​b=logc​alogc​b​

log⁡ambn=nmlog⁡ab\log_a{_mb^n}=\frac nm\log_abloga​m​bn=mn​loga​b

Treat the logarithms like a variable in factorization and expansion.

For the general form

f(x) = k\log_a(bx+c)+d

, we have:

Vertical asymptote: x=−cbx=-\frac cbx=−bc​

Range: {y∣y∈Ry | y∈ ℝy∣y∈R}

For the sign of b, the domain changes:

b>0b>0b>0 ⇒ {x∣x>−cbx | x> -\frac cbx∣x>−bc​}

b<0b<0b<0 ⇒ {x∣x<−cbx | x < -\frac cbx∣x<−bc​}

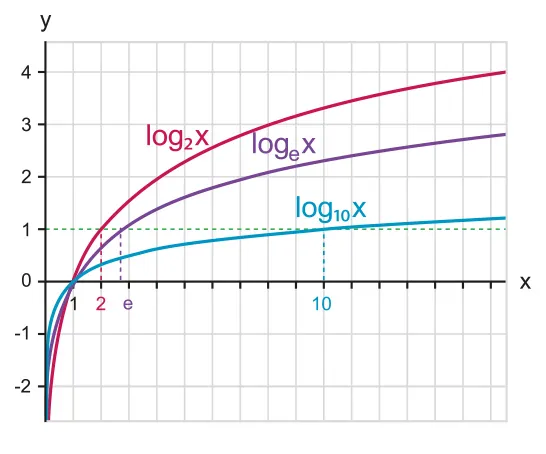
Figure 2.3.2 Logarithm functions with different base values

To solve logarithmic equations, equate the argument with the same base numbers.

*Note that for natural constant

e

, we write:

\log_ex=\ln x