C.3 Wave Phenomena

생성일

2024/07/05 08:37

태그

C.3.1 Wavefronts and rays, Amplitude and Intensity

Wave characteristics and definitions

Terminology	Definition
displacement, $x$	instantaneous distance from equilibrium with direction (change in position); [m]
amplitude, $A$	maximum displacement from the mean position (fixed average point); [m]
frequency, $f$	number of oscillations done per unit time; $[Hz = s^{-1}]$ (cycles per second)
period, $T$	time taken for one complete oscillation; [s] $T=\frac1f$
wave speed, $c$	speed in $ms^{-2}$ at which the wavefronts pass a stationary observer
intensity, $I$	power per unit area that is received by the observer; [ $Wm^{-2}$ ] • intensity is proportional to the square of its amplitude $I ∝ A^{2}$
coherent	when two or more waves are coherent, their frequencies are identical and they have constant phase difference

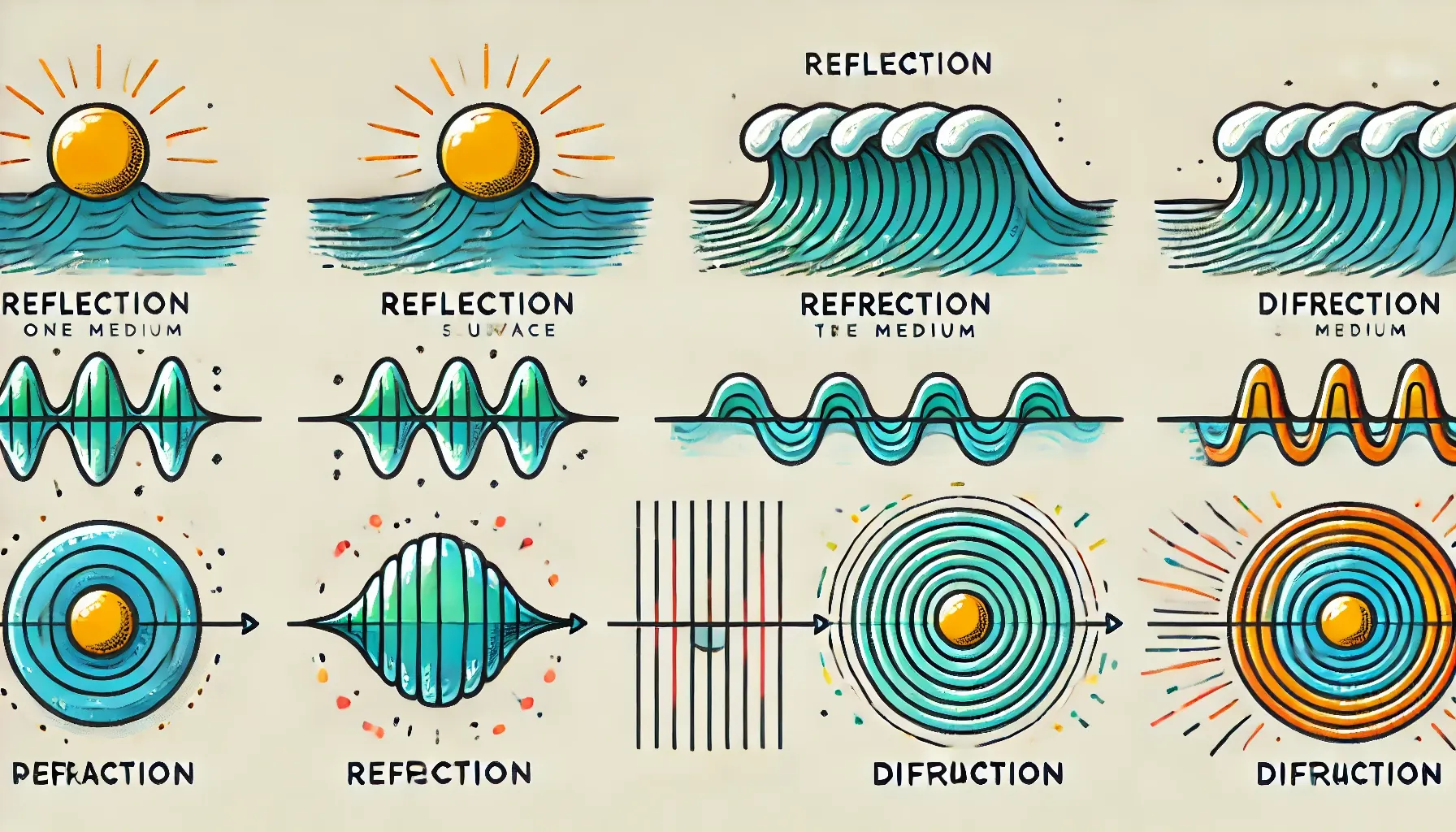
Waves can be described in terms of the motion of a wavefront and/or in terms of rays.

Wavefronts: surface joining neighboring points where oscillations are in phase with each other

•

Can be curves or straight lines

•

Always perpendicular to the direction of wave propagation

C.3.1-1 Diagram of progressing wave with notations

•

(distance between successive wavefronts) = (λ\lambdaλ of the wave)

C.3.1-2 Graph of transverse wave with key-terms notated

Rays: path taken by the wave energy propagation

•

Indicate the direction of wave propagation

•

Are perpendicular to wavefronts

C.3.1-3 Diagram of wave with source at the centre with rays and wavefront

Amplitude and Intensity

•

Amplitude and intensity depends on the energy of the wave.

•

The intensity

•

I is the amount of energy that a wave brings to a unit area every second

◦

Intensity=Power (W)Area (m2)\textit{Intensity} = \frac{\textit{Power} \ (W)}{\textit{Area} \ (m^2)}
Intensity=Area (m2)Power (W)​	Unit : [Wm−2Wm^{-2}Wm−2]

C.3.1-4 dimensional diagram that explaining the intensity in area

•

Power can be defined as amount of energy transmitted per unit time

◦

P=EtP=\frac Et
P=tE​

•

So, intensity is proportional to power

◦

I∝PI∝ PI∝P

•

And in simple harmonic motion, total energy of wave was proportional to amplitude of wave

◦

Etotal=12mω2x02→Etotal∝x02(x0=Amplitude)E_{\text{total}} = \frac{1}{2} m \omega^2 x_0^2 \quad \rightarrow \quad E_{\text{total}} \propto x_0^2 \quad (x_0 = \text{Amplitude})
Etotal​=21​mω2x02​→Etotal​∝x02​(x0​=Amplitude)

◦

I∝Etotal∝x02→I∝x02I \propto E_{\text{total}} \propto x_0^2 \quad \rightarrow \quad I \propto x_0^2I∝Etotal​∝x02​→I∝x02​

•

As a conclusion, intensity is proportional to the square of its amplitude

◦

I∝A2(since E∝A2)I \propto A^2 \quad (\text{since} \ E \propto A^2)I∝A2(since E∝A2)

C.3.1-5 Wave of transverse wave with amplitude notated

Inverse Square Law of Radiation

•

When emitted by a point source S, waves will spread out in all directions, meaning the total energy and power received by the observer will decrease as the energy spreads out over a larger area.

•

Surface area of a sphere of radius r:

A=4\pi r^2

•

The power received per unit area at a distance r away from the point source:

I = \frac{P}{4\pi r^2}

•

Inverse square law: for a given area, the intensity of the received radiation is inversely proportional to the square of the distance from the point source (applied for all waves)

I \propto \frac{1}{r^2}

C.3.1-6 diagram showing the inverse square law in 3D

C.3.2 Superposition

Superposition

•

Waves interfere when two or more coherent waves meet, and the total displacement is the vector sum of their individual displacements.

•

The principle of superposition: the overall displacement at a point where one or more waves interfere is the ‘vector sum’ of the displacement of individual waves

C.3.2-1 graphs showing result of constructive and destructive interference

Types of Interference (Constructive / Destructive)

Constructive Interference

•

path difference : n (n=0,1,2,3,4,5......)

•

phase difference : 0° → in phase

C.3.2-2 Notated Diagram of constructive interference

Destructive Interference

•

path difference :

•

(n+12) (n=0,1,2,3,4,5......)

•

phase difference : 180° () → out of phase

C.3.2-3 Notated Diagram of destructive interference

C.3.3 Polarization

Polarization of waves

•

Polarization only occurs to transverse waves (e.g. light).

•

Polarization of EM waves refers to the orientation of the oscillation in the electric field.

C.3.3-1 Diagram and graph of polarization with notations

•

Unpolarized : vibration varies randomly

•

plane-polarized : fixed plane of vibration

•

Partial polarization: when there is restriction to direction of vibration but not 100%

Polarization by reflection - Brewster’s law

•

The reflected ray is always partially plane-polarized for light incident on the boundary of two media.

•

Reflected ray is totally plane-polarized if the reflected ray and the refracted ray are at 90°.

◦

Polarizing angle: angle of incidence for such condition

C.3.3-2 Digram of reflected and refracted wave with explanations

\theta_i + \theta_r = 90^\circ

•

Brewster’s law relates the refractive index of media, to the incident angle i:

\frac{n_2}{n_1} = \frac{\sin\theta_i}{\sin\theta_r} = \frac{\sin\theta_i}{\cos\theta_i} = \tan\theta_i

•

Thus, when the angle of incidence is equal to Brewster’s angle, the reflected ray is totally polarized and is perpendicular to the refracted ray.

Polarizers and Analyzers

•

Polarizer : any device that produces plane-polarized light from an unpolarized light

◦

Reduces the intensity of unpolarized light by 50%

•

Analyzer : a polarizer used to detect polarized light

◦

When polarized light passes through a polarizer, the intensity is reduced by a factor dependent on the orientation of the polarizer

Malus’ law

•

The preferred direction of the plane-polarized light incident on an analyser will allow a component of light to be transmitted:

C.3.3-3 Diagrams of plane-polarized light with certain angle with notations

•

Intensity of light is proportional to A2A^2A2

◦

Transmitted intensity I∝E2,I0∝E02,I∝E02cos2θ I ∝ E^2, I_0 ∝ E_0^2, I ∝ E_0^2cos^2 \theta
I∝E2,I0​∝E02​,I∝E02​cos2θ

I=I_0cos^2

I=transmitted intensity [

Wm^{-2}

I_0=initial\,incident\,intensity [Wm^{-2}]

\theta=angle between plane of vibration and the analyser's preferred direction

C.3.3-4 Diagram of polarization effect experiment

•

θ=90°→no lighttransmitted by the  analyzer\theta=90° → no\, light transmitted\, by\, the\, analyzer
θ=90°→nolighttransmittedbythe analyzer

C.3.4 Reflection and refraction, Snell's law, critical angle and total internal reflection

Reflection

•

Angle of incidence = Angle of reflection

•

Inverted when reflected from a fixed end, Not inverted when reflected from a free end

C.3.4-1 Notated diagram of reflected wave

Refraction: the change in direction of a wave when it transmits from one medium to another

•

Angle of incidence and refraction can be determined using Snell’s law

Snell's law

\frac{n_1}{n_2} = \frac{\sin\theta_2}{\sin\theta_1} \\ n_1, \, n_2 = \textit{refractive indices of media}

•

Waves move slower in denser media (higher refractive index)

•

fast to slow: transmits towards the normal line, slow to fast: away from normal

C.3.4-2 Digram of refraction with notations

•

Refractive indices n1n_1n1​ and n2n_2n2​ are related by the following equation

\frac{n_1}{n_2} = \frac{\sin\theta_2}{\sin\theta_1} = \frac{\lambda_2}{\lambda_1} = \frac{v_2}{v_1}

C.3.4-3 refracted wave in certain surface with notation

Total internal reflection and critical angle

•

Total internal reflection occurs when the angle of incidence is greater than the critical angle.

\sin\theta_c = \frac{1}{n_1}, \quad \theta_c = \textit{critical angle}

•

It only occurs when the light ray propagates from a optically denser medium to a less dense medium.

C.3.5 Diffraction through a single-slit and around objects

Diffraction: the bending of waves around obstacles in their path

•

Phenomenon where waves spread around obstacles and tend to spread out when they pass through apertures is called diffraction.

•

Wavelength must be of the same order of magnitude as the aperture for noticeable diffraction.

•

Diffraction becomes significant when wavelength becomes relatively large in comparison to the size of the aperture.

•

The frequency, wavelength, speed of waves remains the same after diffraction

•

Direction of propagation changes.

•

Amplitude becomes less than that of the incident wave as energy is distributed over a large area.

C.3.5-1 Single-slit diffraction pattern

C.3.6 Interference patterns, Double-slit interference, Path difference

Interference

•

Maximums are formed at constructive interference and minimums are formed at destructive interference.

C.3.6-1 Interference of light waves

Double-slit interference

•

Double-slit diffraction occurs through the same mechanism of single slit diffraction and interference.

C.3.6-2 wave from two sources

•

If two rays result in a bright patch, then they must arrive in phase.

•

The extra distance that the ray that travels a longer path exceeds is called the path difference.

Path difference=n, n=1, 2, 3, ...

\textit{Path difference} = n\lambda, \quad n = 1, 2, 3, \dots\\ \textit{Also, Path difference} = d \sin\theta\\ n\lambda = d \sin\theta

C.3.6-3 interference of waves from slits with notation

X_n = \frac{n\lambda D}{s}\\ d = X_{n+1} - X_n = \frac{\lambda D}{s}\\ s = \frac{\lambda D}{d}\\ s=distance\, between\, two \, fringes,D=distance\, between \, source\, and\, screen,d=fringe\,  separation

C.3.6-4 Fringe pattern from Young’s Double slit Experiment

The path difference must be:

n\lambda \textit{ where } n = 0, 1, 2, \dots \textit{ for constructive interference}\\ (n + \frac{1}{2})\lambda \textit{ where } n = 0, 1, 2, \dots \textit{ for destructive interference}\\ n \textit{ is the order of the fringe, } n = 0 \textit{ being the zeroth order}

C.3.7 The Nature of Single-Slit Diffraction

The Nature of Single-Slit Diffraction

•

When plane waves are incident normally on a single slit, a diffraction pattern is produced

◦

This is represented as a series of light and dark fringes which show the areas of maximum and minimum intensity

◦

If a laser emitting blue light is directed at a single slit, where the slit width is larger than the wavelength of the light, it will spread out as follows :

C.3.7-1 Combined graph with diagram of Single slit diffraction pattern

•

The features of the single-slit diffraction pattern using monochromatic light :

◦

A central maximum with a high intensity

◦

Equally spaced subsidiary maxima, successively smaller in intensity and half the width of the central maximum

White Light Single Slit Diffraction

C.3.7-2 Diagram of diffraction pattern of white light

•

If the laser were to be replaced by a non-laser source emitting white light :

◦

The central maximum would be white

◦

All maxima would be composed of a spectrum

◦

The shortest wavelength (violet / blue) would appear nearest to the central maximum

◦

The longest wavelength (red) would appear furthest from the central maximum

◦

The fringe spacing would be smaller and the maxima would be wider

Equation in Single Slit Diffraction

•

The relationship between angle of diffraction and wavelength of the light can be represented by equation :

\theta = \frac{\lambda}{2}

•

If refers that the angle if diffraction is directly proportional to the wavelength of the light

C.3.7-3 Annotated diagram of Single slit diffraction

•

From the equation the angle represents the angular separation from cetre to first minimum

•

The equation can be used for second and third minimum appeared at the diffraction pattern

C.3.8 Effect on Intensity of Maxima and Minima

Intesity of Maxima and Minima

•

Using different sources of monochromatic light demonstrates

◦

Increasing the wavelength increases the width of the fringes

•

The angle of diffraction of the first minima can be found using the equation :

\theta = \frac{\lambda}{2}

•

This equation explains why red light produces wider maxima

◦

It is because the longer the wavelength, λ, the larger the angle of diffraction, θ

•

It also explains the coloured fringes seen when white light is diffracted

◦

It is because red light (longer λ) will diffract more than blue light which has shorter wavelength

◦

This creates fringes which are blue nearer the centre and red further out

•

It also explains why wider slits cause the maxima to be narrower

◦

It is because the wider the slit the smaller the angle of diffraction

C.3.8-1 Diffraction pattern

C.3.9 Young’s Double-Slit Experiment

Young’s Double-Slit Experiment

C.3.9-1 annotated diagram of Young’s Double-Slit Experiment

•

When a monochromatic light source is placed behind a single slit, the light is diffracted producing two light sources at the double slits A and B

•

Since both light sources originate from the same primary source, they are coherent and will therefore create an observable interference pattern

◦

Both diffracted light from the double slits create an interference pattern made up of bright and dark fringes

•

By using the trigonometric equations we can evaluate the equation involving wavelength of the light, distance between double slit to screen, fringe width and distance between slits :

C.3.9-2 annotated equation and relative diagram

The Effect of Single slit Diffraction on Young’s Double-Slit Experiment

•

Young’s Double Slit experiment had assumption that the slits are infinitely small that only wavefronts of source pass through the slit

C.3.9-3 Diagram of original fringe pattern

•

This assumption is including that the single wavelet of wavefronts are perfectly spherical and the energy distribution is even over the spherical wavefront

•

It enables each slit to be treated as a point source and the interference pattern considered has regular peak maxima

•

The slits have finite width

◦

This allows that the wavefronts would not perfectly spherical after passing the slits and due to the single slit diffraction effect the intensity distribution is not even

◦

The intensity distribution follow the single slit diffraction pattern

C.3.9-4 annotated diagram of realistic Young’s Double Slit Experiment

◦

This concludes that Young’s double slit experiment entails both features of interference pattern and diffraction pattern

C.3.10 Diffraction Grating

Diffraction Grating Patterns

•

A diffraction grating is a plate consisting of a very large number of parallel, identical, close-spaced slits

C.3.10-1 Diagram of Diffraction Grating Experiment

•

On the diffraction pattern as the number of slits increases (Maxima and Minima) :

◦

Between the maxima, secondary maxima appear

◦

The central maxima and subsequent bright fringes become narrower

C.3.10-2 Diagram of Diffraction Grating results

•

On a diffraction pattern, as the number of slits increases (Intesity) :

◦

The intensity of the central and other larger maxima increases

◦

Since the overall amount of light being let through each slit is increased, the pattern increases in intensity

Equation for Diffraction Grating

•

From the experiment of Diffraction grating

◦

Equation of Diffraction grating can be evaluated including the angular separation between the order of maxima, distance between neighboring slits, wavelength of the source and order of maxima :

C.3.10-3 annotated equation of diffraction grating

C.3.11 Thin Film Effect

Thin Film Effect

•

The effect is caused by the reflection of waves from the top and bottom surface of the thin film

•

For thin film effect to happen :

◦

The film has to have higher refractive index than the medium surrounding it

◦

It has to transmit the light

C.3.11-1 Thin Film diagram

•

When light is incident on the surface A light wave reflects with phase change (wave 1)

◦

Because light wave is experiencing reflection at the boundary between less dense to more dense medium

◦

Involving the diagram above, the light wave on surface A experiences reflection and undergoes a phase change of half a wavelength in terms of path difference and /180° difference in terms of phase difference

•

When refracted light wave is incident on the surface B light wave reflects with no phase chage (wave 2)

◦

Because during the wave is passing through from less dense to more dense medium both reflection and refraction happens

◦

So the part of the light wave passes through the film and incident on the boundary between film and air (surface B)

◦

Then the light wave ib surface B is at the boundary of more dense to less dense medium so the reflection undergoes without a phase change

•

Then after both waves are out of the film (wave 1 and wave 2) they interfere and forms constructive or destructive interference with certain conditions

•

The condition for constructive and destructive interference to happen can be organized by the equation

◦

For constructive interference, normally constructive interference occurs when two waves are in phase

◦

But in this case one of the light wave is already had phase change so the path difference need to be half wavelength

•

So the equation can be established :

2dn = \left(m + \frac{1}{2} \right) \lambda\\ (d = \textit{thickness of the film}, \quad n = \textit{refractive index of medium}, \quad m = \textit{integer})

•

The condition for destructive interference to happen can be organized by the equation

◦

For destrictive interference, it occurs when two waves are out of phase

◦

Because one wave is already had phase change of 180°, so get out of phase again

◦

The path difference should be multiple of wavelength

•

So the equation can be established :

2dn = m\lambda\\ (d = \textit{thickness of the film}, \quad n = \textit{refractive index of medium}, \quad m = \textit{integer})

(d=thicknesso of the film, n=refractive index of medium, m=integer)

•

In case when there is another medium at the bottom of the film with higher refractive index then film

◦

The refracted wave will experience phase change again

◦

So the condition for constructive and destructive index will be exactly opposite