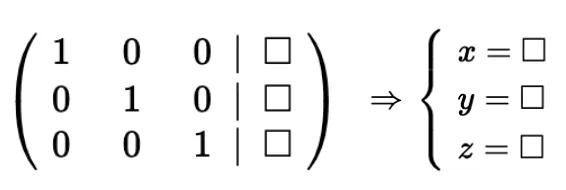Terminology
Definition
System of equations
A system of linear equations consists of two or more linear equations with the same set of variables. The solution to the system is the set of values that satisfy all the equations simultaneously.
Types of solutions:
•
Unique Solution: Occurs when the equations intersect at a single point. The lines/ planes are not parallel.
•
No Solution: Occurs when the equations represent parallel lines/ planes that never intersect. There are no common solutions.
•
Infinite Solutions: Occurs when the equations represent the same line/ plane, meaning all points on the line/ plane are solutions. The lines/ planes coincide.
Systems of equations can be solved by elimination of variables and/ or substitution.
Augmented matrices
An augmented matrix includes the coefficients and the constants of a system of linear equations, separated by a vertical line.
Row operations for
Elementary row operations are used to eliminate variables from an augmented matrix.
Elementary row operations include:
1.
Swapping Rows: Interchanging two rows.
2.
Multiplying a Row by a Constant: Multiplying all elements in a row by a non-zero scalar.
3.
Adding/Subtracting Rows: Adding or subtracting a multiple of one row from another row.
There are three possible outcomes:
Row operations for
Row Echelon Form (REF): The form where the matrix has a leading 1 in each row and zeros below it.
If we reduce the form, the system has a unique solution.
Reduced Row Echelon Form (RREF): A further simplified form where each leading 1 is the only non-zero entry in its column.
Using REF, there are three possible outcomes:
1.
There is a unique triplet of numbers that satisfy all three equations.
2.
There is no triplet of real numbers that satisfy all the equations.
3.
There are infinitely many triplets of real numbers that satisfy all the equations.